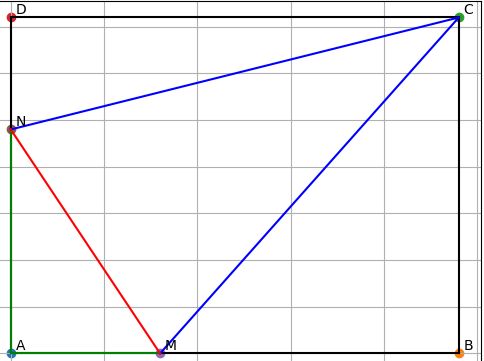
a) Tính diện tích tam giác AMN, MBC, DCN
1. Diện tích tam giác AMN
Trong hình chữ nhật: AB ⊥ AD
→ AM ⊥ AN (vì AM ⊂ AB, AN ⊂ AD).
- Tam giác AMN vuông tại A.
AM = 16, AN = 24
S_AMN = $\frac{1}{2}$.AM.AN = $\frac{1}{2}$.16.24 = 192
2. Diện tích tam giác MBC
Ta có: MB = AB − AM = 48 − 16 = 32, BC = AD = 36
Vì AB ⊥ BC, tam giác MBC vuông tại B.
S_MBC = $\frac{1}{2}$.MB.BC = $\frac{1}{2}$.32.36 = 576​
3. Diện tích tam giác DCN
Ta có:
DN = 12
DC = AB = 48
Vì CD ⊥ AD, tam giác DCN vuông tại D.
S_DCN = $\frac{1}{2}$.DC.DN = $\frac{1}{2}$.48.12 = 288
b) Tính diện tích tam giác MNC
- Ta chia hình chữ nhật thành bốn phần theo 3 tam giác đã tính:
+ Diện tích hình chữ nhật: S_ABCD = AB.AD = 48.36 = 1728
- Ta có: S_MNC = S_ABCD − (S_AMN + S_MBC + S_DCN)
=> Thay số: S_MNC = 1728 − (192 + 576 + 288)
=> S_MNC ​= 672​

Chào bạn! Đây là bài giải chi tiết cho bài toán hình học này.

Đầu tiên, ta cần xác định vị trí của các điểm $M$ và $N$ và tính toán diện tích các tam giác dựa trên diện tích hình chữ nhật $ABCD$.

📐 Phân tích và Tính toán
Hình chữ nhật $ABCD$ có các kích thước:

Chiều dài $AB = 48$
Chiều rộng $AD = 36$
Diện tích hình chữ nhật $ABCD$ là:

$S_{ABCD} = AB \times AD = 48 \times 36 = 1728$
Xác định vị trí các điểm $M$ và $N$
Điểm $M$: $AM = \frac{1}{3} AB$.

$AM = \frac{1}{3} \times 48 = 16$.
Vì $M$ nằm trên $AB$, nên $MB = AB - AM = 48 - 16 = 32$.
Điểm $N$: $N$ nằm trên $AD$ vì $D, N, A$ thẳng hàng theo đề bài cho $ND$ và $AN$. Ta có $ND = \frac{1}{2} AN$.

Đặt $AN = x$. Khi đó $ND = \frac{1}{2} x$.
Vì $N$ nằm trên $AD$, ta có $AN + ND = AD$.
$x + \frac{1}{2} x = 36$
$\frac{3}{2} x = 36$
$x = 36 \times \frac{2}{3} = 24$.
Vậy, $AN = 24$ và $ND = 12$.

a. Tính diện tích tam giác $AMN$, $MBC$, $DCN$
1. Tính diện tích tam giác $AMN$
$AMN$ là tam giác vuông tại $A$.

$S_{AMN} = \frac{1}{2} \times AM \times AN$
$S_{AMN} = \frac{1}{2} \times 16 \times 24$
$S_{AMN} = \frac{1}{2} \times 384 = **192**$.
2. Tính diện tích tam giác $MBC$
$MBC$ là tam giác vuông tại $B$.

$S_{MBC} = \frac{1}{2} \times MB \times BC$

(Vì $BC = AD = 36$)
$S_{MBC} = \frac{1}{2} \times 32 \times 36$
$S_{MBC} = \frac{1}{2} \times 1152 = **576**$.
3. Tính diện tích tam giác $DCN$
$DCN$ là tam giác vuông tại $D$.

$S_{DCN} = \frac{1}{2} \times DC \times DN$

(Vì $DC = AB = 48$ và $DN = 12$)
$S_{DCN} = \frac{1}{2} \times 48 \times 12$
$S_{DCN} = \frac{1}{2} \times 576 = **288**$.

b. Tính diện tích tam giác $MNC$
Diện tích tam giác $MNC$ được tính bằng cách lấy diện tích hình chữ nhật $ABCD$ trừ đi tổng diện tích của ba tam giác vuông đã tính ở trên.

$S_{MNC} = S_{ABCD} - (S_{AMN} + S_{MBC} + S_{DCN})$
$S_{MNC} = 1728 - (192 + 576 + 288)$
$S_{MNC} = 1728 - 1056$
$S_{MNC} = **672**$

📝 Đáp số
$S_{AMN} = 192$ (đơn vị diện tích)
$S_{MBC} = 576$ (đơn vị diện tích)
$S_{DCN} = 288$ (đơn vị diện tích)
$S_{MNC} = 672$ (đơn vị diện tích)