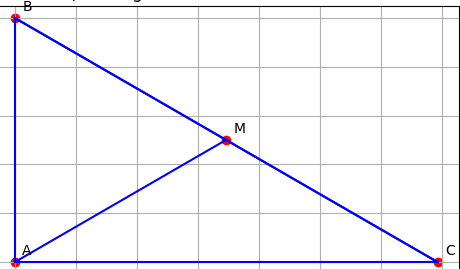
cho tam giác ABC vuông tại A có B=60 . trên cạch BC lấy điểm M sao cho góc CAM = 30 . Chứng minh rằng :
a ) Tam giác CAM cân tại M
b) Tam giác BAN là tam giác đều
c) M là trung điểm của đoạn thẳng BC
Quảng cáo
4 câu trả lời 186
a) Chứng minh tam giác CAM cân tại M
Trong tam giác ABC, có:
= 30°
= 30° (theo đề)
Vì M nằm trên BC, nên tia AM chia góc C thành: = 30∘ = .
Xét tam giác CAM, ta có:
30°
30°
Hai góc ở C và M bằng nhau ⇒ đối diện chúng là các cạnh bằng nhau: CM = AM.
⇒ Tam giác CAM cân tại M.
b) Chứng minh tam giác BAM là tam giác đều
Xét tổng góc tam giác ABC:
= 90°
= 60°
Ở phần a, ta có: AM = CM. Ta lại có góc CAM = 30° nên:
0 = 1 = 60∘ − 30∘ = 30∘.
- Trong tam giác BAM:
2 (góc vuông)
0 = 30° ⇒ suy ra 4 = 60°.
Tổng ba góc: 30∘ + 60∘ + 90∘ = 180∘ (hợp lý)
Suy ra:
5 = 60°
630°
4 = 60°
Xét tam giác BAM:
860°
4 = 60°
Hai góc bằng nhau ⇒ cạnh đối diện bằng nhau: BA = AM
Mà ta cũng có: 0⇒ Tam giác BAM có 3 góc 60° ⇒ là tam giác đều.
c) Chứng minh M là trung điểm BC
Ta đã có:
AM = CM (ở (a))
AM = BM (ở (b), vì tam giác BAM đều)
Suy ra: BM = AM = CM.
Do đó: BM = MC. ⇒ M là trung điểm BC.
**Cho tam giác ABC vuông tại A, ∠B = 60°, ∠C = 30°.
Trên BC lấy điểm M sao cho ∠CAM = 30°.**
a) Chứng minh tam giác CAM cân tại M
Vì tam giác ABC vuông tại A:
⇒ ∠B = 60°, ∠C = 30°.
Xét tam giác ABC: cạnh đối góc 30° là cạnh nhỏ nhất →
AB = AC √3 và AC = AB√3 (tỉ lệ 30°–60°–90° quen thuộc).
Có ∠C = 30°, mà ∠CAM = 30° (theo đề).
⇒ ∠MAC = ∠ACM.
→ Trong tam giác CAM, hai góc ở M và A bằng nhau → tam giác CAM cân tại M.
=> CM = AM. ✔️
b) Chứng minh tam giác BAM đều
Ta đã biết:
∠B = 60°.
∠CAM = 30°.
Nhưng ∠C = 30° nên đường thẳng AM chia ∠C thành 30° và 0°? Không phải, ta phải nhìn góc tại A:
Trong tam giác ABC vuông tại A:
∠A = 90°.
Ta có:
∠CAM = 30° (theo đề)
→ ∠BAM = 90° – 30° = 60°.
⇒ Tam giác BAM có:
∠B = 60°
∠A = 60°
Tổng góc tam giác = 180° → ∠M = 60°
→ Cả 3 góc đều 60° → tam giác BAM đều. ✔️
c) Chứng minh M là trung điểm BC
Ta có:
Tam giác CAM cân tại M nên CM = AM
Tam giác BAM đều nên AM = BM
Kết hợp lại:
CM = AM
AM = BM
⇒ CM = BM
→ M là điểm chia BC thành hai đoạn bằng nhau.
→ M là trung điểm BC.
Phân tích và Chứng minh
Bước 1: Tính toán các góc trong $\triangle ABC$
Vì $\triangle ABC$ vuông tại A, ta có $\angle BAC = 90^\circ$. Ta có $\angle B = 60^\circ$. Suy ra $\angle C = 180^\circ - 90^\circ - 60^\circ = 30^\circ$.
Ta có $\angle BAM = \angle BAC - \angle CAM = 90^\circ - 30^\circ = 60^\circ$.
a) Chứng minh tam giác CAM cân tại M
Xét tam giác CAM, ta có:
(\angle C = 30^\circ) (Tính toán ở trên).
$\angle CAM = 30^\circ$ (Theo giả thiết).
Vì (\angle C = \angle CAM = 30^\circ), nên tam giác CAM là tam giác cân tại đỉnh đối diện với góc bằng nhau. Cạnh đối diện với (\angle C) là $AM$. Cạnh đối diện với $\angle CAM$ là $CM$. Do đó, $AM = CM$.
Kết luận a): $\triangle CAM$ cân tại M (vì có hai cạnh kề với góc $\angle AMC$ bằng nhau là $AM=CM$).
b) Chứng minh tam giác BAN là tam giác đều
Lưu ý: Trong đề bài không có thông tin về điểm N. Dựa trên các tính toán góc ở trên ((\angle BAM = 60^\circ)), khả năng cao đây là lỗi đánh máy và đề bài muốn chứng minh tam giác BAM là tam giác đều. Ta sẽ chứng minh điều này.
Chứng minh $\triangle BAM$ là tam giác đều (Giả sử $N=M$): Xét tam giác BAM, ta có:
$\angle B = 60^\circ$ (Theo giả thiết).
$\angle BAM = 60^\circ$ (Tính toán ở Bước 1). Suy ra $\angle AMB = 180^\circ - 60^\circ - 60^\circ = 60^\circ$.
Vì cả ba góc của $\triangle BAM$ đều bằng $60^\circ$, nên $\triangle BAM$ là tam giác đều. Do đó, $AB = AM = BM$.
c) Chứng minh M là trung điểm của đoạn thẳng BC
Để M là trung điểm của BC, ta cần chứng minh $BM = MC$.
Từ kết quả của Phần a), ta có: $AM = CM$.
Từ kết quả chứng minh Phần b) (với giả định $\triangle BAM$ đều), ta có: $AM = BM$.
Từ (1) và (2), ta suy ra $BM = CM$.
Kết luận c): $M$ là trung điểm của đoạn thẳng $BC$.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11452
Đã trả lời bởi chuyên gia
11452 -
 Đã trả lời bởi chuyên gia
8620
Đã trả lời bởi chuyên gia
8620 -
 Đã trả lời bởi chuyên gia
5846
Đã trả lời bởi chuyên gia
5846