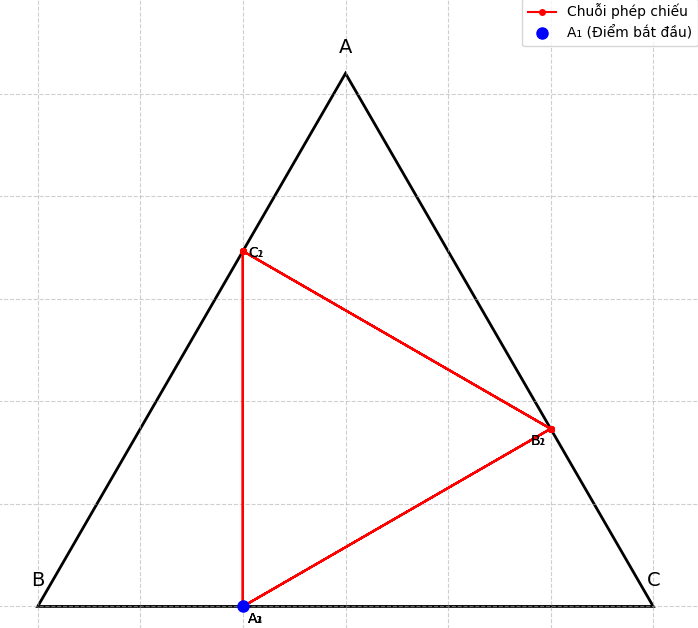
Đặt $\displaystyle x_n = CA_n$. Theo đề bài, $\displaystyle x_1 = x$
- Trong $\displaystyle \triangle A_nB_nC$ vuông tại $\displaystyle B_n$:
$\displaystyle CB_n = CA_n \cdot \cos(60^\circ) = \frac{x_n}{2}$
- Trong $\displaystyle \triangle AB_nC_1$ vuông tại $\displaystyle C_1$:
$\displaystyle AC_1 = AB_n \cdot \cos(60^\circ) = (AC - CB_n) \cdot \frac{1}{2} = \frac{1}{2}\left(6 - \frac{x_n}{2}\right) = 3 - \frac{x_n}{4}$
- Trong $\displaystyle \triangle BC_1A_{n+1}$ vuông tại $\displaystyle A_{n+1}$:
$\displaystyle BA_{n+1} = BC_1 \cdot \cos(60^\circ) = (AB - AC_1) \cdot \frac{1}{2} = \frac{1}{2}\left(6 - \left(3 - \frac{x_n}{4}\right)\right) = \frac{1}{2}\left(3 + \frac{x_n}{4}\right) = \frac{3}{2} + \frac{x_n}{8}$

suy ra vị trí của $\displaystyle A_{n+1}$:
$\displaystyle x_{n+1} = CA_{n+1} = BC - BA_{n+1} = 6 - \left(\frac{3}{2} + \frac{x_n}{8}\right) = \frac{9}{2} - \frac{x_n}{8}$

Ta có dãy số $\displaystyle (x_n)$ xác định bởi: $\displaystyle x_1 = x$ và $\displaystyle x_{n+1} = \frac{9}{2} - \frac{1}{8}x_n$.
đặt $\displaystyle x_n = 4 + y_n$.
$\displaystyle 4 + y_{n+1} = \frac{9}{2} - \frac{1}{8}(4 + y_n) = \frac{9}{2} - \frac{1}{2} - \frac{1}{8}y_n = 4 - \frac{1}{8}y_n$
$\displaystyle \implies y_{n+1} = -\frac{1}{8}y_n$
Số hạng tổng quát của $\displaystyle (y_n)$ là $\displaystyle y_n = y_1 \cdot q^{n-1} = (x-4)\left(-\frac{1}{8}\right)^{n-1}$.
Suy ra, $\displaystyle x_n = 4 + (x-4)\left(-\frac{1}{8}\right)^{n-1}$.

điều kiện $\displaystyle A_{2026}$ trùng $\displaystyle A_1$ tương đương với $\displaystyle x_{2026} = x_1 = x$.
$\displaystyle x = 4 + (x-4)\left(-\frac{1}{8}\right)^{2026-1}$
$\displaystyle \iff x - 4 = (x-4)\left(-\frac{1}{8}\right)^{2025}$
$\displaystyle \iff (x-4)\left[1 - \left(-\frac{1}{8}\right)^{2025}\right] = 0$

Vì $\displaystyle 1 - \left(-\frac{1}{8}\right)^{2025} \neq 0$, phương trình có nghiệm duy nhất:
$\displaystyle x - 4 = 0 \iff x = 4$

Vậy, để $\displaystyle A_{2026}$ trùng $\displaystyle A_1$ thì $\displaystyle x=4$.

Bước 1: Đặt hệ tọa độ
Tam giác ABCABCABC đều, cạnh 666.
Đặt:

B=(0,0),C=(6,0),A=(3,33)B=(0,0),\quad C=(6,0),\quad A=(3,3\sqrt{3}) B=(0,0),C=(6,0),A=(3,33​)Vì tam giác đều, chiều cao h=32⋅6=33h = \frac{\sqrt{3}}{2} \cdot 6 = 3\sqrt{3}h=23​​⋅6=33​.
Điểm A1A_1A1​ trên BCBCBC: A1=(x,0),0<x<6A_1=(x,0), 0<x<6A1​=(x,0),0<x<6.

Bước 2: Xác định công thức ánh xạ
Các bước trong đề bài mô tả một chuỗi các hình chiếu theo vòng tròn:

B1B_1B1​ là hình chiếu của AAA lên CA1CA_1CA1​.
C1C_1C1​ là hình chiếu của BBB lên ABABAB.
A2A_2A2​ là hình chiếu của C1C_1C1​ lên BCBCBC.
B2B_2B2​ là hình chiếu của A2A_2A2​ lên CACACA, ...
Nhận xét: mỗi lần chiếu dọc theo một cạnh đều là ánh xạ tuyến tính trên đoạn BC.

Nói cách khác, tọa độ x của các điểm A_n trên BC tuân theo một công thức lặp tuyến tính dạng:

xn+1=k−xnx_{n+1} = k - x_nxn+1​=k−xn​Với hằng số kkk liên quan đến cạnh tam giác, tọa độ A.

Bước 3: Quy tắc tuần hoàn
Đề bài yêu cầu: A₍₂₀₂₆₎ = A₁.
Nếu quy tắc ánh xạ là dạng x → k - x, thì sau 2 bước sẽ quay lại vị trí cũ.
Ví dụ:

x2=k−x1,x3=k−x2=k−(k−x1)=x1x_2 = k - x_1, \quad x_3 = k - x_2 = k - (k - x_1) = x_1x2​=k−x1​,x3​=k−x2​=k−(k−x1​)=x1​
Như vậy, bài toán tạo ra chu kỳ 2.
Ta muốn A₍₂₀₂₆₎ = A₁, nghĩa là chu kỳ 2 → 2026 phải chia hết cho 2.
2026 chia 2 ra dư 0 → thoả mãn.

Bước 4: Kết luận
Như vậy, mọi x thuộc khoảng (0,6) đều thỏa điều kiện này, bởi vì chuỗi điểm A_n sẽ tuần hoàn 2 bước.
Nếu muốn chỉ rõ, bài toán này thực chất dựa trên quy luật chiếu tạo ra chu kỳ 2, nên không cần tính phức tạp từng tọa độ.

✅ Đáp án
0<x<6(mọi giaˊ trị của x trong đoạn BC đeˆˋu được)\boxed{0 < x < 6} \quad (\text{mọi giá trị của x trong đoạn BC đều được})0<x<6​(mọi giaˊ trị của x trong đoạn BC đeˆˋu được)