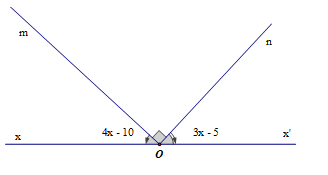
Bài 1: Cho hình vẽ dưới đây,biết: Góc xOz = 150 độ và góc xOy - góc yOz = 90 độ. Tính số đo các góc: x'Oy; xOy và yOz
Bài 2:
Cho Góc MON = 120 độ . Vẽ OP và OQ nằm giữa hai tia OM và ON sao cho OP vuông góc với OM; OQ vuông góc với ON
a) So sánh Góc MOQ và Góc NOP
b) Tính số đo Góc POQ
Quảng cáo
3 câu trả lời 248
Bài 1:
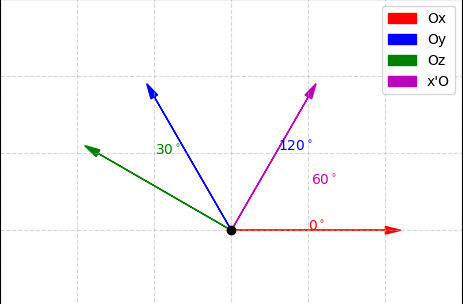
Vì chưa có hình, ta giả sử là góc kề bù với góc , tức:
= 180∘ −
Ta biết: − = 90∘ ⟹ = + 90∘
Tổng góc: = + = 150∘
Thay: = + 90∘ vào: ( + 90∘) + = 150∘
⇒ 2. + 90∘ = 150∘
=> 2. = 60∘ ⟹ 7 = 30∘
+ Tính : = + 90∘ = 30∘ + 90∘ = 120∘
+ Tính : = 180∘ − = 180∘ − 120∘ = 60∘
=> Kết quả: = 60∘, = 120∘ , = 30∘
Bài 2:
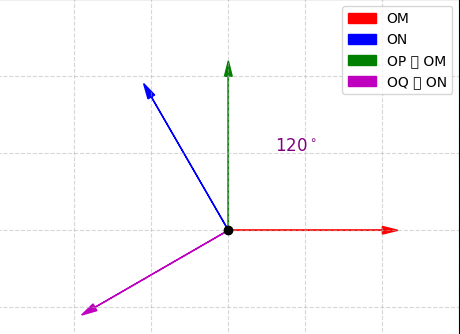
a) So sánh 7 và 8:
OM và ON tạo góc 120∘.
OP ⊥ OM → 9 = 90∘
OQ ⊥ ON → 0 = 90∘
Tia OP nằm trong 1, cách tia OM một góc 90∘
Tương tự, OQ cách tia ON một góc 90∘.
Góc 7là góc giữa hai tia OM và OQ.
Góc 8là góc giữa hai tia ON và OP.
Do OQ ⊥ ON nên góc 7 = 1 − 90∘ = 120∘ − 90∘ = 30∘.
Do OP ⊥ OM, góc 8 = 90∘.
Vậy: 7 = 30∘ < 8 = 90∘
b) Tính số đo góc 9:
9 là góc giữa hai tia OP và OQ.
=> 9 = 180∘ − 1 = 180∘ − 120∘= 60∘ (Do OP ⊥ OM, OQ ⊥ ON, nên 9 là góc ngoài góc 1 và bằng 180∘ − 120∘).
Đầu tiên, tôi sẽ giải Bài 1, sau đó sẽ giải Bài 2.
Bài 1:
Tính số đo các góc: x'Oy; xOy và yOz
Để giải bài toán này, chúng ta sẽ sử dụng các tính chất của các góc trên một đường thẳng và các hệ phương trình.
Theo hình vẽ, ta có:
Hai góc kề bù là xOy và x′Oy nên xOy +x′Oy =180∘.
Hai góc kề nhau là xOy và yOz nên xOy +yOz =xOz .
Ta có hệ phương trình sau:
xOy +yOz =150∘ (vì xOz =150∘)
xOy −yOz =90∘
Cộng hai phương trình trên, ta được:
(xOy+yOz)+(xOy−yOz)=150∘+90∘
2xOy=240∘
xOy=120∘
Thay xOy=120∘ vào phương trình (1), ta có:
120∘+yOz=150∘
yOz=150∘−120∘=30∘
Ta có xOy+x′Oy=180∘ (hai góc kề bù).
120∘+x′Oy=180∘
x′Oy=180∘−120∘=60∘
Vậy:
x′Oy =60∘
xOy =120∘
yOz =30∘
Bài 2:
Cho Góc MON = 120 độ . Vẽ OP và OQ nằm giữa hai tia OM và ON sao cho OP vuông góc với OM; OQ vuông góc với ON
a) So sánh Góc MOQ và Góc NOP
Ta có:
Vì OP vuông góc với OM nên MOP =90∘.
Vì OQ vuông góc với ON nên NOQ =90∘.
Vì OP và OQ nằm giữa hai tia OM và ON nên ta có:
MOQ =MON −NOQ =120∘−90∘=30∘
NOP =MON −MOP =120∘−90∘=30∘
Vậy MOQ =NOP =30∘.
b) Tính số đo Góc POQ
Ta có:
MON =MOP +POQ +QON
MON =120∘
MOP =90∘
QON =90∘
Tuy nhiên, cách trên không chính xác vì các góc không kề nhau. Ta phải sử dụng cách sau:
POQ=MON−MOP−NOQ là sai.
Vì tia OP nằm giữa hai tia OM và ON nên MON=MOP+PON.
PON=MON−MOP=120∘−90∘=30∘.
Vì tia OQ nằm giữa hai tia OM và ON nên MON=MOQ+QON.
MOQ=MON−QON=120∘−90∘=30∘.
Ta có: POQ =MON −MOP −NOQ là sai.
Ta có:
MON=MOQ+QON=MOQ+90∘⟹MOQ=120∘−90∘=30∘
MON=MOP+PON=90∘+PON⟹PON=120∘−90∘=30∘
Do OP và OQ nằm giữa hai tia OM và ON nên ta có:
POQ=MON−MOP−NOQ
POQ=MON−(MOP+NOQ) là sai.
Ta có:
POQ=MON−MOP−NOQ là sai.
Đúng ra là:
Vì tia OQ nằm giữa hai tia OM và ON nên tia OQ nằm giữa hai tia OM và OP (nếu MOQ<MOP) hoặc tia OP nằm giữa hai tia OM và OQ (nếu MOQ>MOP).
MOQ=30∘ và MOP=90∘, vậy tia OQ nằm giữa hai tia OM và OP.
MOP=MOQ+QOP
90∘=30∘+QOP
QOP=90∘−30∘=60∘
Vậy POQ =60∘.
Đầu tiên, tôi sẽ giải Bài 1, sau đó sẽ giải Bài 2.
Bài 1:
Tính số đo các góc: x'Oy; xOy và yOz
Để giải bài toán này, chúng ta sẽ sử dụng các tính chất của các góc trên một đường thẳng và các hệ phương trình.
Theo hình vẽ, ta có:
Hai góc kề bù là xOy và x′Oy nên xOy +x′Oy =180∘.
Hai góc kề nhau là xOy và yOz nên xOy +yOz =xOz .
Ta có hệ phương trình sau:
xOy +yOz =150∘ (vì xOz =150∘)
xOy −yOz =90∘
Cộng hai phương trình trên, ta được:
(xOy+yOz)+(xOy−yOz)=150∘+90∘
2xOy=240∘
xOy=120∘
Thay xOy=120∘ vào phương trình (1), ta có:
120∘+yOz=150∘
yOz=150∘−120∘=30∘
Ta có xOy+x′Oy=180∘ (hai góc kề bù).
120∘+x′Oy=180∘
x′Oy=180∘−120∘=60∘
Vậy:
x′Oy =60∘
xOy =120∘
yOz =30∘
Bài 2:
Cho Góc MON = 120 độ . Vẽ OP và OQ nằm giữa hai tia OM và ON sao cho OP vuông góc với OM; OQ vuông góc với ON
a) So sánh Góc MOQ và Góc NOP
Ta có:
Vì OP vuông góc với OM nên MOP =90∘.
Vì OQ vuông góc với ON nên NOQ =90∘.
Vì OP và OQ nằm giữa hai tia OM và ON nên ta có:
MOQ =MON −NOQ =120∘−90∘=30∘
NOP =MON −MOP =120∘−90∘=30∘
Vậy MOQ =NOP =30∘.
b) Tính số đo Góc POQ
Ta có:
MON =MOP +POQ +QON
MON =120∘
MOP =90∘
QON =90∘
Tuy nhiên, cách trên không chính xác vì các góc không kề nhau. Ta phải sử dụng cách sau:
POQ=MON−MOP−NOQ là sai.
Vì tia OP nằm giữa hai tia OM và ON nên MON=MOP+PON.
PON=MON−MOP=120∘−90∘=30∘.
Vì tia OQ nằm giữa hai tia OM và ON nên MON=MOQ+QON.
MOQ=MON−QON=120∘−90∘=30∘.
Ta có: POQ =MON −MOP −NOQ là sai.
Ta có:
MON=MOQ+QON=MOQ+90∘⟹MOQ=120∘−90∘=30∘
MON=MOP+PON=90∘+PON⟹PON=120∘−90∘=30∘
Do OP và OQ nằm giữa hai tia OM và ON nên ta có:
POQ=MON−MOP−NOQ
POQ=MON−(MOP+NOQ) là sai.
Ta có:
POQ=MON−MOP−NOQ là sai.
Đúng ra là:
Vì tia OQ nằm giữa hai tia OM và ON nên tia OQ nằm giữa hai tia OM và OP (nếu MOQ<MOP) hoặc tia OP nằm giữa hai tia OM và OQ (nếu MOQ>MOP).
MOQ=30∘ và MOP=90∘, vậy tia OQ nằm giữa hai tia OM và OP.
MOP=MOQ+QOP
90∘=30∘+QOP
QOP=90∘−30∘=60∘
Vậy POQ =60∘.
Quảng cáo
Bạn muốn hỏi bài tập?