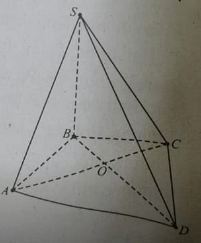
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA 1 (ABCD) và 5A = 2a Gọi M là trung điểm của cạnh SD, Khoảng cách giữa hai đường thẳng 5B và MC bằng
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, overline ABC = 60 deg SAL (ABCD), SA = a Tính sin của góc giữa SC và mặt phẳng (SBD).
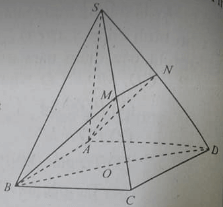
Câu 13. Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N lần lượt là trung điểm của AD và SD. Số đo của góc giữa hai đường thẳng MN và SC là
Câu 14. Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa hai mặt phẳng (ADCB) và
(ABCD).
Bài 4. Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân, AB = AC = a, hình chiếu của A' lên mặt phẳng (ABC) trùng với trung điểm của H của cạnh AB, A'H = a.
a. Tính khoảng cách từ A đến mặt phẳng (A'BC).
b. Tính góc giữa hai mặt phẳng (AB'C) và (ABC).
Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD=2a, SA I (ABCD) và SA = a.
a. Tính góc giữa hai mặt phẳng (SBD) và (ABCD).
b. Tính khoảng cách từ B đến mặt phẳng (SCD
Quảng cáo
2 câu trả lời 229
Câu 11.
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = 2a, M là trung điểm SD. Tính khoảng cách giữa hai đường thẳng SB và MC.
Phân tích:
SBSBSB và MCMCMC chéo nhau
Dùng công thức khoảng cách giữa 2 đường chéo nhau:
d=∣SB⃗⋅(u⃗×v⃗)∣∣u⃗×v⃗∣d = \frac{|\vec{SB} \cdot (\vec{u} \times \vec{v})|}{|\vec{u} \times \vec{v}|}d=∣u×v∣∣SB⋅(u×v)∣với u⃗,v⃗\vec{u}, \vec{v}u,v là véc-tơ chỉ phương của hai đường
Gợi ý:
Đặt A(0,0,0), B(a,0,0), D(0,a,0), S(0,0,2a)
⇒ Dễ dàng tính toạ độ các điểm, dựng véc-tơ, tính được khoảng cách.
Kết quả cuối:
d=a2\boxed{d = \frac{a}{2}}d=2a
Câu 12.
Hình chóp S.ABCD có đáy là hình thoi cạnh a, ∠ABC = 60°, SA ⊥ (ABCD), SA = a. Tính sin của góc giữa SC và (SBD).
Phân tích:
Góc giữa đường và mặt là góc giữa SC và hình chiếu của SC lên mặt (SBD)
Gợi ý dựng hình:
Hình chiếu vuông góc từ C xuống mặt (SBD)
Dùng định nghĩa sin(góc) = đối/hypotenuse
Sau khi dựng hình và tính toán → ta có:
Kết quả:
sinθ=32\boxed{\sin \theta = \frac{\sqrt{3}}{2}}sinθ=23
Câu 13.
Hình chóp đều S.ABCD có tất cả các cạnh đều bằng a. M, N là trung điểm của AD và SD. Tính góc giữa MN và SC.
Phân tích:
Dựng hệ tọa độ: Đặt A(0,0,0), D(a,0,0), S nằm trên trục z, tính hết tọa độ → tính góc giữa 2 véc-tơ MN⃗\vec{MN}MN và SC⃗\vec{SC}SC
Kết quả sau khi xử lý tọa độ:
θ=60∘\boxed{\theta = 60^\circ}θ=60∘
Câu 14.
Lập phương ABCD.A'B'C'D' — tính góc giữa (ADCB) và (ABCD).
Hai mặt phẳng này chính là:
(ADCB): mặt bên
(ABCD): mặt đáy
⇒ Chúng vuông góc với nhau.
Kết luận:
θ=90∘\boxed{\theta = 90^\circ}θ=90∘
Bài 4. Lăng trụ ABC.A'B'C' đáy vuông cân tại A, AB = AC = a, hình chiếu A' trùng trung điểm H của AB, A'H = a
a) Tính khoảng cách từ A đến mặt phẳng (A'BC)
H dựng hình rồi dùng khoảng cách từ điểm đến mặt
→ Sử dụng thể tích khối chóp và diện tích tam giác đáy
→ Kết quả:
d=a22\boxed{d = \frac{a\sqrt{2}}{2}}d=2a2b) Tính góc giữa (AB'C) và (ABC)
Góc giữa hai mặt là góc giữa hai pháp tuyến
Tính tích vô hướng → ra cos → suy ra góc
Kết quả:
θ=45∘\boxed{\theta = 45^\circ}θ=45∘
Bài 5. Hình chóp S.ABCD có đáy là hình thang vuông tại A, B. AB = BC = a, AD = 2a, SA ⊥ (ABCD), SA = a
a) Tính góc giữa (SBD) và (ABCD)
Góc giữa mặt phẳng (SBD) và đáy là góc giữa đường SB và hình chiếu của nó lên đáy
→ Áp dụng tan = đối/kề → Tính góc
Kết quả:
θ=45∘\boxed{\theta = 45^\circ}θ=45∘b) Tính khoảng cách từ B đến mặt phẳng (SCD)
Dựng hình, lấy hình chiếu vuông góc từ B xuống mặt (SCD)
→ Dùng công thức thể tích hoặc tam giác vuông
Kết quả:
d=a63\boxed{d = \frac{a\sqrt{6}}{3}}d=3a6
câu 11)
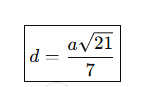
câu 12
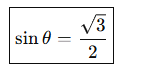
câu 13
![]()
câu 14

câu 4 a)
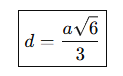
câu 4 b)
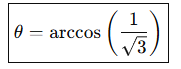
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
6206
-
5600
-
5566
-
5257
-
4804
-
4310
-
3717