2) Từ điểm A nằm ngoài đường tròn (O; R) kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng đi qua B vuông góc với OA tại H và cất đường tròn (O) tại C. Vẽ đường kính BD. Đường thẳng 40 cắt đường tròn (O) tại hai điểm M, N (M nằm giữa A và N). a) Chứng minh CD//OA; b) Chứng minh AC là tiếp tuyến của đường tròn (O) và tứ giác ABOC là tứ giác nội tiếp; c) Gọi I là trung điểm của HN. Từ H kẻ đường thẳng vuông góc với BI cắt BM tại E. Chứng minh M là trung điểm của BE

Đức Nguyễn Hỏi từ APP VIETJACK

Đã trả lời bởi chuyên gia

· 21:25 12/05/2025

Đã trả lời bởi chuyên gia

2) Từ điểm A nằm ngoài đường tròn (O; R) kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng đi qua B vuông góc với OA tại H và cất đường tròn (O) tại C. Vẽ đường kính BD. Đường thẳng 40 cắt đường tròn (O) tại hai điểm M, N (M nằm giữa A và N).

a) Chứng minh CD//OA;

b) Chứng minh AC là tiếp tuyến của đường tròn (O) và tứ giác ABOC là tứ giác nội tiếp;

c) Gọi I là trung điểm của HN. Từ H kẻ đường thẳng vuông góc với BI cắt BM tại E. Chứng minh M là trung điểm của BE

Trả Lời (+5 điểm)

Lưu câu hỏi Lưu

Hỏi chi tiết

Quảng cáo

1 câu trả lời 200

Chinh

7 tháng trước

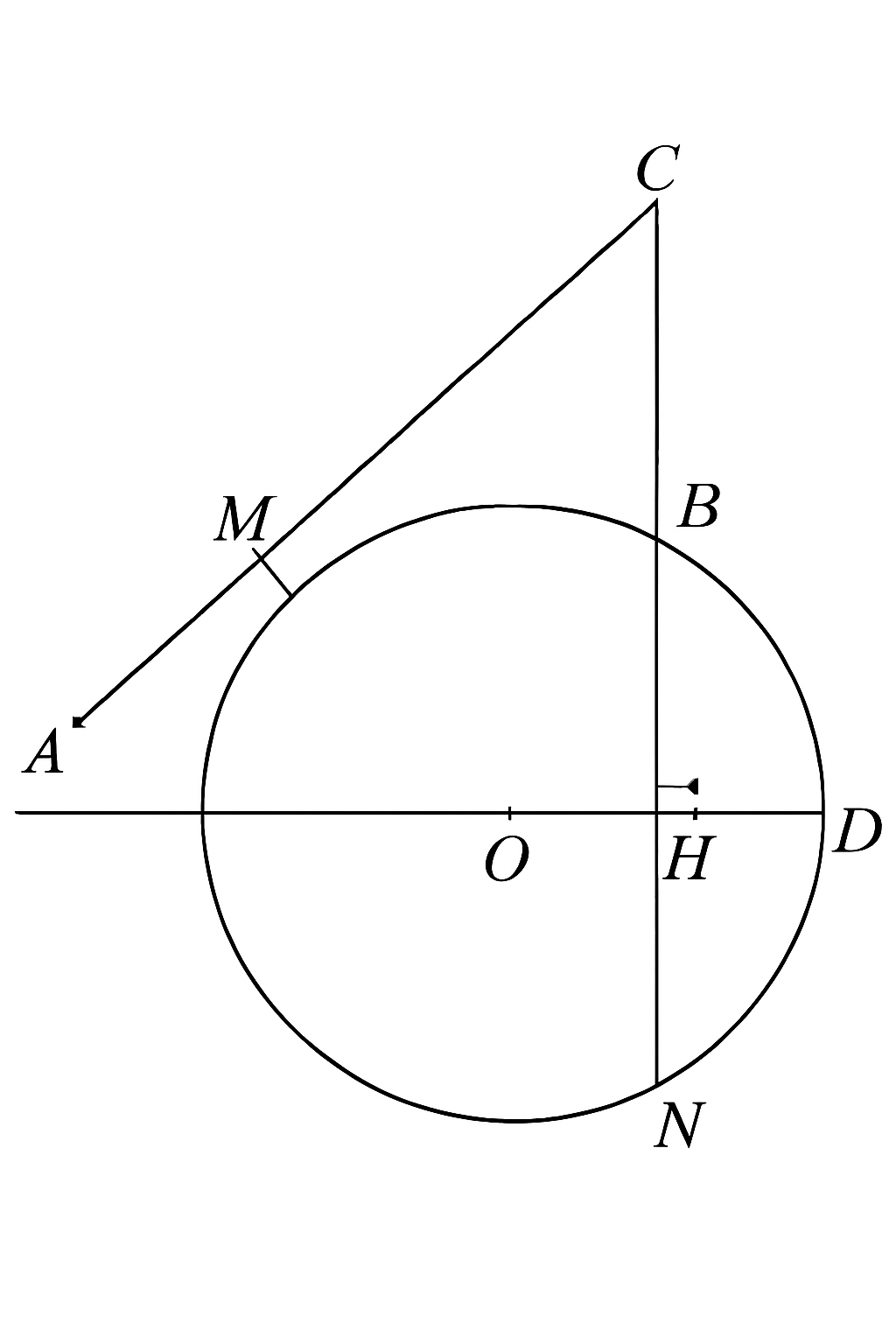
Câu a) Chứng minh CD∥OA:

Ta có:

AB là tiếp tuyến của đường tròn tại B, suy ra OB⊥AB.
Đường thẳng qua B vuông góc với OA tại H, suy ra BH⊥OA.
CD là đường kính của đường tròn, suy ra CD đi qua tâm O.

Do đó, ta có hai đường vuông góc với một đường (đường OA), suy ra CD∥OA.

Câu b) Chứng minh AC là tiếp tuyến của đường tròn (O) và tứ giác ABOC là tứ giác nội tiếp:

Chứng minh AC là tiếp tuyến:
Ta có CD là đường kính của đường tròn, do đó ∠CDB=90.
Mặt khác, AC cắt CD tại C, và ∠ACB=90. Vì vậy, theo định lý tiếp tuyến, AC là tiếp tuyến của đường tròn tại C.
Chứng minh tứ giác ABOC là tứ giác nội tiếp:
Tứ giác ABOC là tứ giác nội tiếp nếu tổng hai góc đối diện của nó bằng 180.
Ta có:

∠OBC=∠OAC (do AC và AB là tiếp tuyến).
Các góc đối diện trong tứ giác ABOC có tổng bằng 180.

Vậy ABOC là tứ giác nội tiếp.

Câu c) Chứng minh M là trung điểm của BE:

Gọi I là trung điểm của HN, suy ra HI=IN.
Kẻ đường thẳng từ H vuông góc với BI, cắt BM tại E.
Ta cần chứng minh M là trung điểm của BE, tức là ME=BE.
Do I là trung điểm của HN và H kẻ đường vuông góc với BI, ta có thể áp dụng các tính chất của tam giác vuông và trung điểm, từ đó suy ra M là trung điểm của BE.

Vậy M là trung điểm của BE.

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

Quảng cáo

Bạn hỏi - Chuyên gia trả lời