a) SA và mặt phẳng (SBC).
b) SD và mặt phẳng (SAC)
Giải theo cách lớp 11
Quảng cáo
1 câu trả lời 531
Câu a: Tính \( \sin \angle(SA, (SBC)) \)
- Gọi \( \alpha \) là góc giữa \( SA \) và mặt phẳng \( (SBC) \)
- \( \sin \alpha = \dfrac{|\vec{SA} \times \vec{n}|}{|\vec{SA}||\vec{n}|} \), với \( \vec{n} \) là vector pháp tuyến mặt SBC
### Tìm vector:
\[
\vec{SA} = A - S = (0 - 0, 0 - a, 0 - a\sqrt{\frac{2}{3}}) = (0, -a, -a\sqrt{\frac{2}{3}})
\]
Mặt SBC có hai vector:
\[
\vec{SB} = (a, -a, -a\sqrt{\frac{2}{3}}),\quad \vec{SC} = (a, a, -a\sqrt{\frac{2}{3}})
\]
Tính tích có hướng:
\[
\vec{n} = \vec{SB} \times \vec{SC}
= \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a & -a & -a\sqrt{\frac{2}{3}} \\
a & a & -a\sqrt{\frac{2}{3}} \\
\end{vmatrix}
\]
Tính:
- i: \( (-a)(-a\sqrt{2/3}) - (-a)(-a\sqrt{2/3}) = 0 \)
- j: \( a(-a\sqrt{2/3}) - a(-a\sqrt{2/3}) = 0 \)
- k: \( a \cdot a - (-a)(a) = a^2 + a^2 = 2a^2 \)
\[
\vec{n} = (0, 0, 2a^2)
\]
→ Pháp tuyến vuông góc mặt phẳng SBC, hướng thẳng trục z
Tính góc giữa \( SA \) và mặt phẳng SBC → chính là góc giữa \( \vec{SA} \) và vector pháp tuyến \( \vec{n} \)
\[
\sin \alpha = \dfrac{|\vec{SA} \cdot \vec{n}|}{|\vec{SA}||\vec{n}|}
\]
\[
\vec{SA} = (0, -a, -a\sqrt{2/3}),\quad \vec{n} = (0, 0, 2a^2)
\]
\[
\vec{SA} \cdot \vec{n} = -a\sqrt{2/3} \cdot 2a^2 = -2a^3\sqrt{2/3}
\Rightarrow |\vec{SA} \cdot \vec{n}| = 2a^3\sqrt{2/3}
\]
\[
|\vec{SA}| = \sqrt{a^2 + a^2\cdot \frac{2}{3}} = \sqrt{a^2\left(1 + \frac{2}{3}\right)} = a\sqrt{\frac{5}{3}}
\]
\[
|\vec{n}| = 2a^2
\]
\[
\sin \alpha = \dfrac{2a^3\sqrt{2/3}}{a\sqrt{5/3} \cdot 2a^2} = \dfrac{\cancel{2}a^3\sqrt{2/3}}{\cancel{2}a^3\sqrt{5/3}} = \dfrac{\sqrt{2/3}}{\sqrt{5/3}} = \sqrt{\frac{2}{5}} = \boxed{\dfrac{\sqrt{10}}{5}}
\]
Câu b: Tính \( \sin \angle(SD, (SAC)) \)
Làm tương tự:
\[
\vec{SD} = (0, a, -a\sqrt{2/3})
\]
Mặt phẳng SAC → chọn 2 vector:
- \( \vec{SA} = (0, -a, -a\sqrt{2/3}) \)
- \( \vec{SC} = (a, a, -a\sqrt{2/3}) \)
Tính tích có hướng:
\[
\vec{n'} = \vec{SA} \times \vec{SC}
= \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
0 & -a & -a\sqrt{2/3} \\
a & a & -a\sqrt{2/3} \\
\end{vmatrix}
\]
- i: \( (-a)(-a\sqrt{2/3}) - (-a)(-a\sqrt{2/3}) = 0 \)
- j: \( 0 \cdot (-a\sqrt{2/3}) - a(-a\sqrt{2/3}) = a^2\sqrt{2/3} \)
- k: \( 0 \cdot a - (-a)(a) = a^2 \)
\[
\vec{n'} = (0, a^2\sqrt{2/3}, a^2)
\]
Tính góc giữa \( SD \) và mặt SAC:
\[
\vec{SD} = (0, a, -a\sqrt{2/3})
\]
\[
\vec{SD} \cdot \vec{n'} = a \cdot a^2\sqrt{2/3} + (-a\sqrt{2/3}) \cdot a^2 = a^3\sqrt{2/3} - a^3\sqrt{2/3} = 0
\]
→ Góc giữa \( \vec{SD} \) và mặt phẳng SAC là 90°
\[
\boxed{\sin = 1}
\]
Đáp số:
a) \( \boxed{\sin \angle(SA, (SBC)) = \dfrac{\sqrt{10}}{5}} \)
b) \( \boxed{\sin \angle(SD, (SAC)) = 1} \)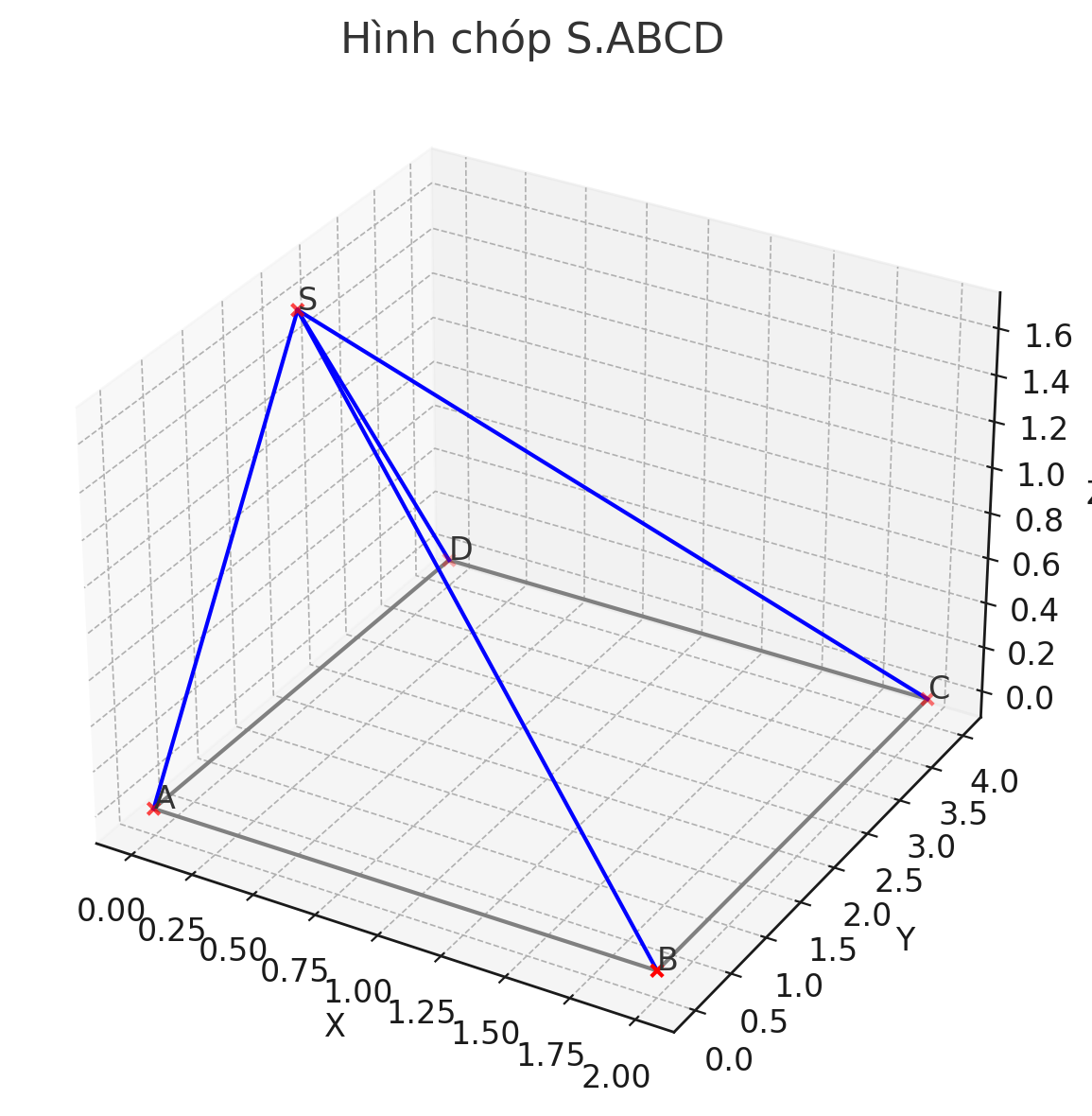
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK72718
-
56040
-
Hỏi từ APP VIETJACK40676
-
Hỏi từ APP VIETJACK37754


