Cho tam giác ABC vuông tại B phân giác AD kẻ DE vuông góc AC E thuộc AC Chứng minh a tam giác Bad bằng tam giác ed B AD là trung trực của Be c Trên tia đối của tia pe c Trên tia đối của tia BA lấy điểm K giao cho BK = CE Chứng minh ba điểm ed k thẳng hàng

Thy Trần Hỏi từ APP VIETJACK

· 13:30 11/04/2025

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

2 câu trả lời 692

Sang Phạm

8 tháng trước

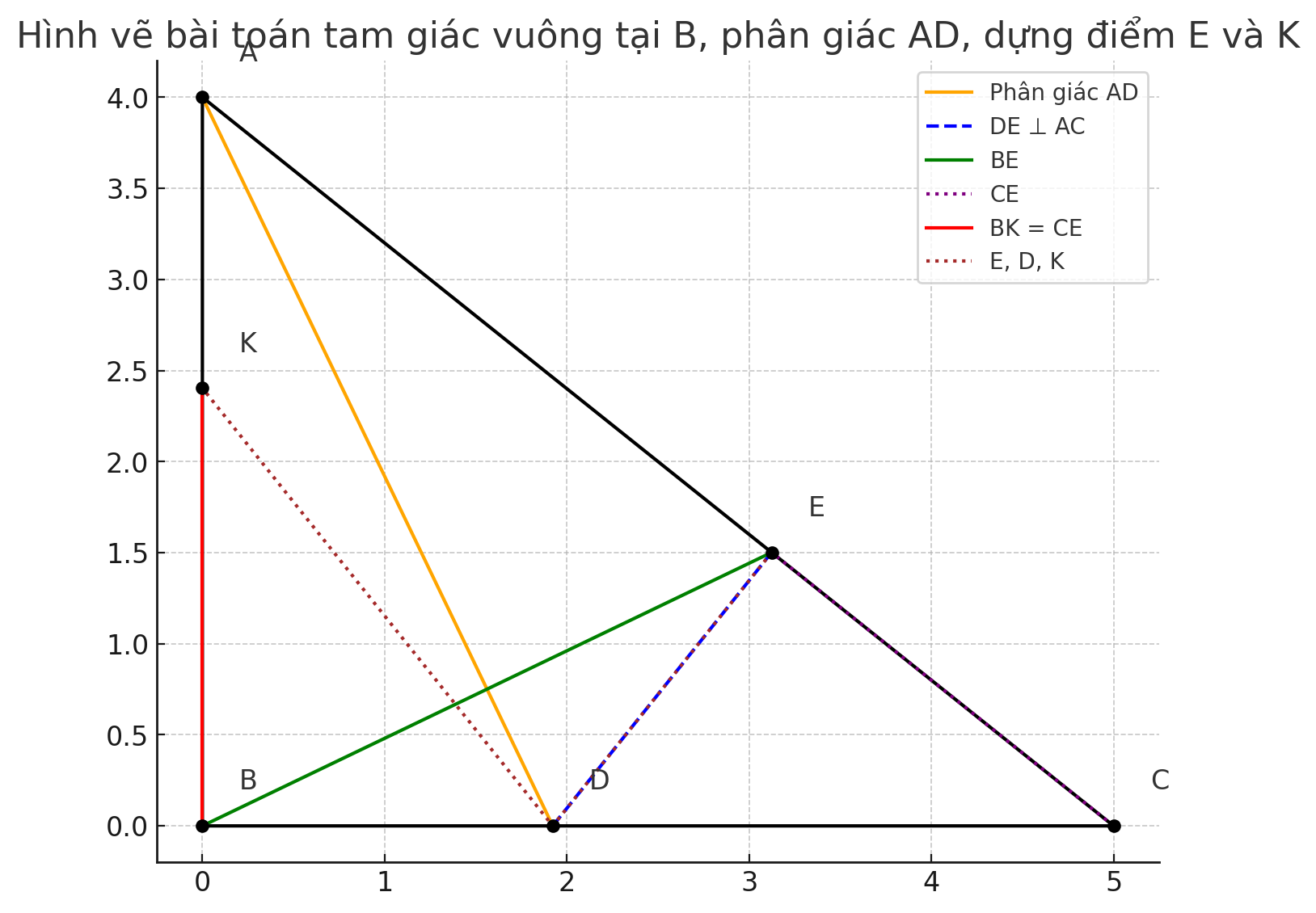
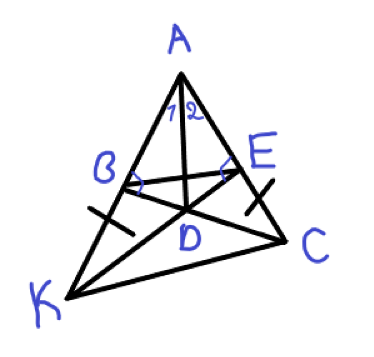
Câu a: Chứng minh tam giác BAD = tam giác EDB

Giải:

Xét tam giác BAD và tam giác EDB, ta có:
- ∠ADB chung
- DE ⊥ AC ⇒ ∠EDB = 90°, tam giác EDB vuông tại D
- Tam giác ABC vuông tại B ⇒ ∠ABD = 90°, tam giác ABD vuông tại B
- AD là phân giác ⇒ chia ∠A thành 2 góc bằng nhau
⇒ Xét ∆BAD và ∆EDB có:
- BD chung
- ∠ABD = ∠EDB = 90°
- ∠ADB chung

⇒ ∆BAD = ∆EDB (g.c.g)

Câu b: Chứng minh AD là trung trực của BE

Giải

Từ câu a, ∆BAD = ∆EDB ⇒
- AB = EB
- ∠BAD = ∠EDB ⇒ hai tam giác đối xứng nhau qua đường AD
⇒ A nằm đối xứng E qua đường AD ⇒ AD là trung trực của BE

Câu c:
Trên tia đối của tia BA, lấy điểm K sao cho BK = CE. Chứng minh 3 điểm E, D, K thẳng hàng

Giải:

- Từ b: AD là trung trực của BE ⇒ ∆BED cân tại D
- BK = CE (giả thiết)
- Từ tam giác cân ∆BED, nếu CE = BK và lại có D là trung điểm của BE (vì AD là trung trực), thì D cũng sẽ là trung điểm của EK
⇒ Tức là: E, D, K thẳng hàng (theo tính chất trung điểm của đoạn thẳng)

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

vu duy anh

8 tháng trước

Tam giác ABC vuông tại B, nên AD là phân giác của góc BAC.
Vì DE vuông góc với AC, nên tam giác BAD và tam giác EAD có cùng một góc (góc BAD = góc EAD).
Hai tam giác này còn có cùng một cạnh chung là AD, nên theo định lý về sự tương đương của tam giác, tam giác BAD = tam giác EAD.
b.

Vì tam giác BAD = tam giác EAD, nên các cạnh tương ứng bằng nhau, trong đó AB = AE.
Theo tính chất của phân giác, AD là trung trực của BE.
c.

Vì tam giác BAD = tam giác EAD, nên các cạnh tương ứng bằng nhau, trong đó AB = AE.
Theo tính chất của phân giác, AD là trung trực của BE.
Trên tia đối của tia BA, lấy điểm K sao cho BK = CE.
Vì AD là trung trực của BE, nên ED = EB.
Vì BK = CE, nên tam giác BKC = tam giác BEC (cạnh-cạnh-cạnh).
Như vậy, các điểm E, D, K thẳng hàng

1 bình luận