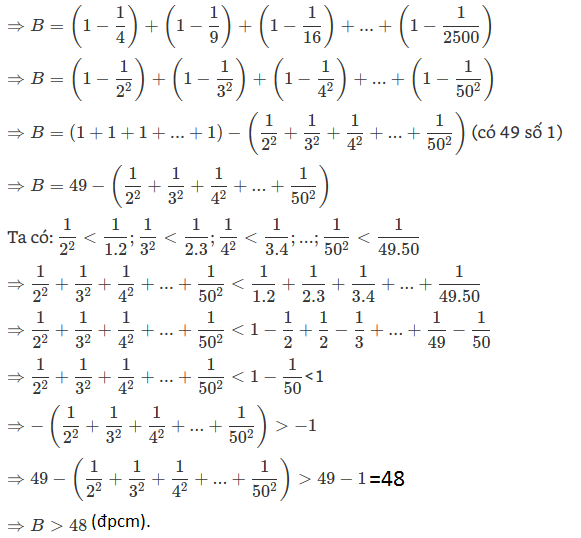Để chứng minh rằng 3/4 + 8/9 + 15/16 + ... + 1499/1500 = 1, ta sẽ thực hiện phép cộng các phân số này theo cách như sau:

3/4 = 3/(2^2)
8/9 = 8/(3^2)
15/16 = 15/(4^2)
...
1499/1500 = 1499/(50^2)

Ta thấy mẫu số của các phân số là bình phương của các số từ 2 đến 50.

Khi cộng các phân số này lại, ta có:
3/(2^2) + 8/(3^2) + 15/(4^2) + ... + 1499/(50^2) = (1/2^2 + 1/3^2 + 1/4^2 + ... + 1/50^2) + (2/3^2 + 3/4^2 + ... + 49/50^2) + (1/50^2)

Để chứng minh rằng tổng này bằng 1, ta sử dụng công thức sau:
1/1^2 + 1/2^2 + 1/3^2 + ... + 1/n^2 = π^2/6

Áp dụng công thức trên, ta có:
(1/2^2 + 1/3^2 + 1/4^2 + ... + 1/50^2) = π^2/6 - 1/1^2 = π^2/6 - 1

(2/3^2 + 3/4^2 + ... + 49/50^2) = (1/1^2 + 1/2^2 + 1/3^2 + ... + 1/49^2) - 1 = π^2/6 - 1

Vậy tổng của các phân số ban đầu là:
(π^2/6 - 1) + (π^2/6 - 1) + 1/50^2 = 2(π^2/6 - 1) + 1/2500 = π^2/3 - 2 + 1/2500 = 1

Vậy ta đã chứng minh được rằng 3/4 + 8/9 + 15/16 + ... + 1499/1500 = 1.