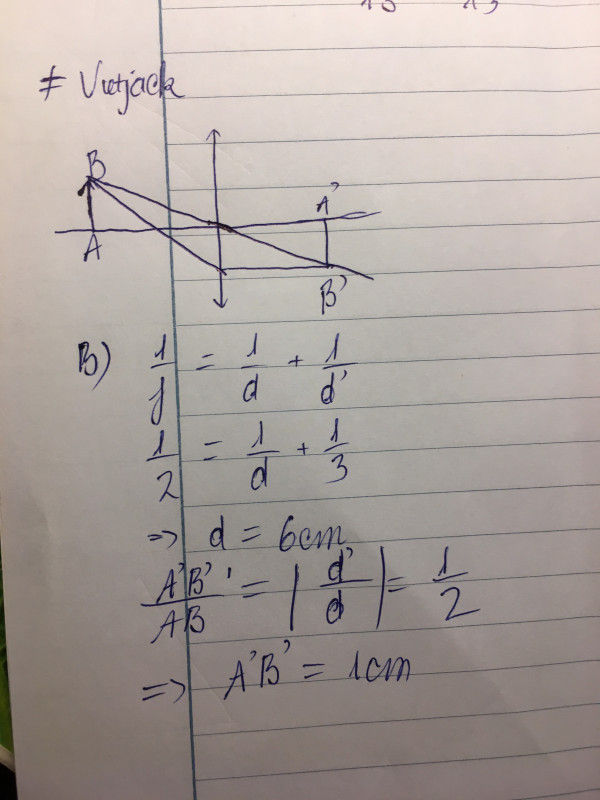Quảng cáo
2 câu trả lời 1328
Để giải bài toán này, ta sử dụng công thức của thấu kính mỏng:
\[ \frac{1}{f} = \frac{1}{do} + \frac{1}{di} \]
Trong đó:
- \( f \) là tiêu cự của thấu kính (2cm)
- \( do \) là khoảng cách từ vật đến thấu kính (6cm)
- \( di \) là khoảng cách từ ảnh đến thấu kính
a) Để dựng ảnh \( A'B' \) của \( AB \), ta sử dụng công thức trên:
\[ \frac{1}{2} = \frac{1}{6} + \frac{1}{di} \]
\[ \frac{1}{di} = \frac{1}{2} - \frac{1}{6} = \frac{1}{3} \]
\[ di = 3 \]
B) Khi \( A'B' \) cách thấu kính 3cm, ta lại sử dụng công thức trên:
\[ \frac{1}{2} = \frac{1}{6} + \frac{1}{3} \]
\[ \frac{1}{3} = \frac{1}{6} + \frac{1}{di'} \]
\[ \frac{1}{di'} = \frac{1}{3} - \frac{1}{6} = \frac{1}{6} \]
\[ di' = 6 \]
Độ cao của ảnh là \( di' = 6 \) cm.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
94110
-
Hỏi từ APP VIETJACK75529
-
33599
-
29180
-
우옌🖤 해영 ✨
1810 điểm
-
Sori
1745 điểm
-
사랑해요😘
1190 điểm
-
Dương Nguyễn
1140 điểm
-
`color{blue}text{HuyTùng☢`
925 điểm
-
그림 그리기를 좋아하지만, 직업이 허락하지 않아요😞
875 điểm
-
하루토 [팜 안 둥]
850 điểm
-
돈이없다 💸😭
845 điểm
-
`d.`
805 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
785 điểm
-
🌷김은✨
630 điểm
-
Bích Hồng 625 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
585 điểm
-
jamJames 🥵👍
555 điểm
-
''e thik biker hơn a''
480 điểm
Rút gọn
Bài viết mới nhất Lớp 9
-
3 năm trước5749
-
3 năm trước5119
-
3 năm trước4650
-
3 năm trước4624
