Cho hàm số:

$y=x^3+\left(m+3\right)x^2+1-m$ (m là tham số)

có đồ thị $\left(C_m\right)$.

Xác định m để đồ thị $\left(C_m\right)$ cắt trục hoành tại x = -2

Cho hàm số $y=\frac{1}{4}{x}^4+\frac{1}{2}{x}^2+m$

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.

Tìm các tiệm cận đứng và ngang của đồ thị hàm số: $y=\frac{x^2+x+1}{3-2x-5x^2}$

Tìm các tiệm cận của đồ thị hàm số: $y=\frac{2x-5}{5x-2}$

Tìm các tiệm cận của đồ thị hàm số:$y=\frac{-x+7}{x+1}$

Tính $li{m}_{n\to 0}\left(\frac{1}{x}+2\right)$ và nêu nhận xét về khoảng cách MH khi x → 0 (H.17)

Trong tất cả các hình chữ nhật có diện tích $48m^2$, hãy xác định hình chữ nhật có chu vi nhỏ nhất.

Tính giá trị lớn nhất của các hàm số sau: $y=\frac{4}{1+x^2}$

Tính giá trị lớn nhất và nhỏ nhất của hàm số:

$y=x^3-3x^2-9x+35$ trên các đoạn [-4; 4] và [0; 5

Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm s f(x) = x(x^2 – 3).

Giả sử f(x) đạt cực đại tại xo. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số $\frac{f\left(x_o+∆x\right)-f\text{'}\left(x_o\right)}{∆x}$ khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.

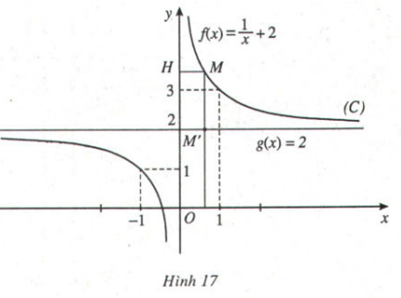
Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):

y = x/3(x+ 3)2 trong các khoảng (1/2; 3/2) và (3/2; 4)

Chứng minh rằng hàm số $y=\frac{x}{x^2+1}$ đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).

Tìm các khoảng đơn điệu của các hàm số:$y=\sqrt{x^2-x-20}$

Xét sự đồng biến, nghịch biến của hàm số: $y=-x^3+x^2-5$

Khẳng định ngược lại với định lí trên có đúng không ? Nói cách khác, nếu hàm số đồng biến (nghịch biến) trên K thì đạo hàm của nó có nhất thiết phải dương (âm) trên đó hay không ?