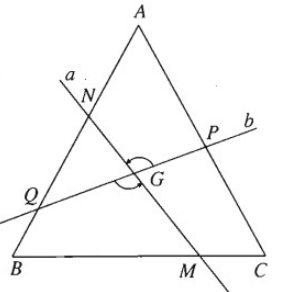
Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng . Chứng minh rằng tứ giác MNPQ là một hình thang cân.
Quảng cáo
1 câu trả lời 337
Gọi là phép quay tâm G góc . Phép quay này biến b thành a, biến CA thành AB; do đó nó biến P thành N.
Tương tự cũng biến Q thành M. Từ đó suy ra GP = GN, GQ = GM. Do đó hai tam giác GNQ và GPM bằng nhau, suy ra NQ = PM. Vì biến PQ thành NM nên PQ = NM. Từ đó suy ra hai tam giác NQM và PMQ bằng nhau. Do đó ∠NQM = ∠PMQ. Tương tự ∠QNP = ∠MPN.
Từ đó suy ra
Do đó NP // QM. Vậy ta có tứ giác MPNQ là hình thang cân.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
19082
Đã trả lời bởi chuyên gia
19082 -
 Đã trả lời bởi chuyên gia
Đã trả lời bởi chuyên gia
Xác định a để 3 số : theo thứ tự lập thành một cấp số cộng?
A. Không có giá trị nào của a
B. a=0
C.
D.
14892 -
 Đã trả lời bởi chuyên gia
10300
Đã trả lời bởi chuyên gia
10300