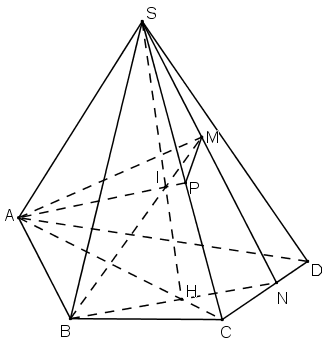
Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD.
a) Tìm giao điểm N của đường thẳng CD và mp(SBM).
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC).
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC).
d) Tìm giao điểm P của SC và mặt phẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM).
Quảng cáo
1 câu trả lời 1848
a) SM, CD cùng thuộc (SCD) và không song song.
Gọi N là giao điểm của SM và CD.
⇒ N ∈ CD và N ∈ SM
Mà SM ⊂ (SMB)
⇒ N ∈ (SMB)
⇒ N = (SMB) ∩ CD.
b) N ∈ CD ⊂ (ABCD)
⇒ BN ⊂ (ABCD)
⇒ AC; BN cùng nằm trong (ABCD) và không song song
Gọi giao điểm của AC và BN là H.
+ H ∈ AC ⊂ (SAC)
+ H ∈ BN ⊂ (SBM)
⇒ H ∈ (SAC) ∩ (SBM)
D
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
19082
Đã trả lời bởi chuyên gia
19082 -
 Đã trả lời bởi chuyên gia
Đã trả lời bởi chuyên gia
Xác định a để 3 số : theo thứ tự lập thành một cấp số cộng?
A. Không có giá trị nào của a
B. a=0
C.
D.
14892 -
 Đã trả lời bởi chuyên gia
10300
Đã trả lời bởi chuyên gia
10300