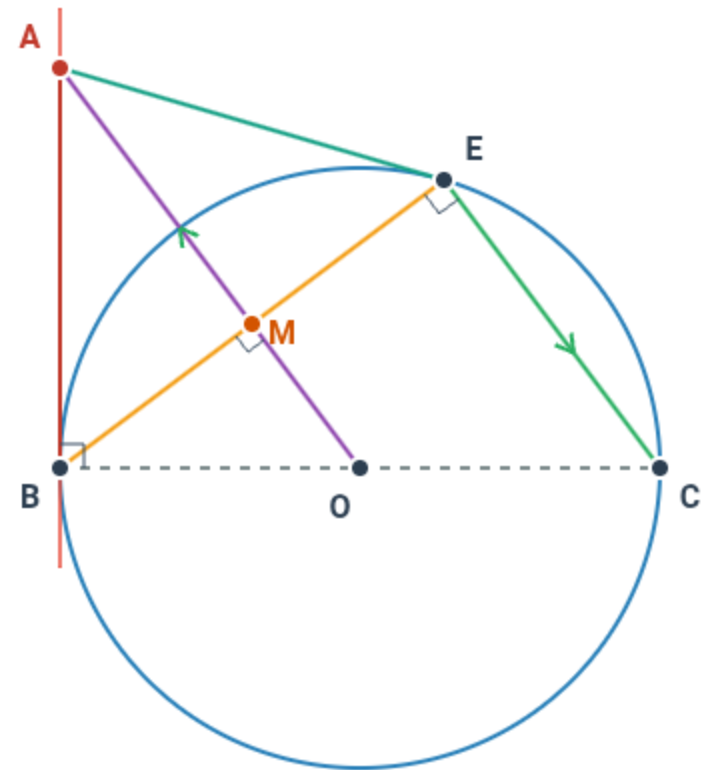
a)

$\displaystyle \text{BC là đường kính nên } \widehat{BEC} = 90^\circ \text{ (góc nội tiếp chắn nửa đường tròn).}$

$\displaystyle\Rightarrow BE \perp EC.$

$\displaystyle \text{Mà } OA \parallel EC \text{ (gt) nên } OA \perp BE \text{ tại } M.$

$\displaystyle \text{Xét } \triangle OAB \text{ và } \triangle OEC:$

$\displaystyle AB\text{ là tiếp tuyến tại B } \Rightarrow OB \perp AB \Rightarrow \triangle OAB \text{ vuông tại B.}$

$\displaystyle\text{Có } OA \parallel EC \Rightarrow \widehat{AOB} = \widehat{OCE} \text{ (đồng vị).}$

$\displaystyle\text{Mà } OC = OE = R \Rightarrow \triangle OCE \text{ cân tại O } \Rightarrow \widehat{OCE} = \widehat{OEC}.$

$\displaystyle\text{Suy ra } \widehat{AOB} = \widehat{OEC}.$

$\displaystyle \text{Xét } \triangle OAB \text{ vuông tại B và } \triangle OEA:$

$\displaystyle OA\text{ chung}, OB = OE = R, \widehat{AOB} = \widehat{OEA} \text{ (do } \widehat{AOB} = \widehat{OEC} = \widehat{OEA}\text{).}$

$\displaystyle\Rightarrow \triangle OAB = \triangle OAE \text{ (cạnh huyền – góc nhọn).}$

$\displaystyle\Rightarrow \widehat{OEA} = \widehat{OBA} = 90^\circ.$

$\displaystyle\text{Vậy } AE \perp OE \text{ tại E, suy ra AE là tiếp tuyến của (O).}$

b)

$\displaystyle \text{Tam giác OAB vuông tại B: } OA = \sqrt{OB^2 + AB^2} = \sqrt{6^2 + 8^2} = 10 \text{ cm.}$

$\displaystyle \text{Áp dụng hệ thức lượng trong } \triangle OAB \text{ vuông tại B, đường cao BM:}$

$\displaystyle OB^2= OM \cdot OA$

$\displaystyle\Rightarrow 6^2 = OM \cdot 10$

$\displaystyle\Rightarrow OM = \frac{36}{10} = 3.6 \text{ cm.}$

$\displaystyle \text{Vậy } OM = 3.6 \text{ cm.}$

Phân tích giả thiết:
Đường tròn $(O; R)$ có đường kính $BC$, suy ra $O$ là trung điểm $BC$ và $OB = OC = R = 6$ cm.
$Ax$ là tiếp tuyến tại $B$ nên $AB \perp BC$.
$CE // OA$.
$M = OA \cap BE$.

a) Chứng minh $AO \perp BE$ và $AE$ là tiếp tuyến của $(O)$
1. Chứng minh $AO \perp BE$:

Xét đường tròn $(O)$, góc $\widehat{BEC}$ là góc nội tiếp chắn nửa đường tròn đường kính $BC$, nên $\widehat{BEC} = 90^\circ$ hay $CE \perp BE$.
Theo giả thiết, $OA // CE$.
Từ quan hệ giữa tính vuông góc và tính song song: Vì $CE \perp BE$ và $OA // CE$ nên $AO \perp BE$ (tại $M$).
2. Chứng minh $AE$ là tiếp tuyến của $(O)$:

Xét $\triangle OBE$ có $OB = OE = R$, nên $\triangle OBE$ cân tại $O$.
Trong tam giác cân $OBE$, $OM$ là đường cao (vì $AO \perp BE$), đồng thời cũng là đường phân giác. Suy ra $\widehat{BOA} = \widehat{EOA}$.
Xét $\triangle ABO$ và $\triangle AEO$ có:

$OB = OE = R$
$\widehat{BOA} = \widehat{EOA}$ (chứng minh trên)
$OA$ là cạnh chung
Do đó $\triangle ABO = \triangle AEO$ (c.g.c).
Suy ra $\widehat{ABO} = \widehat{AEO}$. Mà $\widehat{ABO} = 90^\circ$ (do $AB$ là tiếp tuyến), nên $\widehat{AEO} = 90^\circ$.
Vậy $AE \perp OE$ tại $E$, chứng tỏ $AE$ là tiếp tuyến của đường tròn $(O)$.

b) Tính độ dài đoạn thẳng $OM$
Để tính $OM$, chúng ta sẽ sử dụng hệ thức lượng trong tam giác vuông $ABO$.

Tính độ dài $OA$:

Xét $\triangle ABO$ vuông tại $B$ (do $AB$ là tiếp tuyến):

$AB = 8$ cm
$OB = R = 6$ cm
Áp dụng định lý Pythagoras:

$OA^2 = AB^2 + OB^2 = 8^2 + 6^2 = 64 + 36 = 100$
$\Rightarrow OA = \sqrt{100} = 10 \text{ cm}$
Tính độ dài $OM$:

Xét $\triangle ABO$ vuông tại $B$, có $BM$ là đường cao ứng với cạnh huyền $OA$ (vì $AO \perp BE$ tại $M$):

Theo hệ thức lượng: $OB^2 = OM \cdot OA$
Thay số: $6^2 = OM \cdot 10$
$36 = OM \cdot 10$
$\Rightarrow OM = 3,6 \text{ cm}$

Kết quả:

a) Đã chứng minh $AO \perp BE$ và $AE$ là tiếp tuyến.
b) $OM = 3,6 \text{ cm}$.