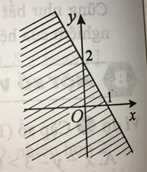
vẽ đồ thị hàm số y =ax2 + bx + c ( a khác 0 ) câu d . x2 - 6x + 5
Quảng cáo
3 câu trả lời 68
y(2)=−4⇔a.22+b.2+c2=−4⇔4a+2b+c=−8 (1).
y(2)=4⇔a.22+b.2+c2=4⇔4a−2b+c=−8 (2).
y=a.x2+b.x+cx=ax+b+cx, suy ra y′=a−cx2.
Ta có y′(2)=0⇔a−ca2=0⇔4a−c=0 (3).
Giải hệ các phương trình (1), (2), (3) ta được a = -1, b = 0, c = -4.
Do đó y=−x2−4x=−x−4x.
limx→±∞[f(x)−(−x)]=limx→±∞[−x−4x−(−x)]=limx→±∞−4x=0.
Vậy đường tiệm cận xiên là y = -x.
Bạn muốn vẽ đồ thị hàm số \( y = ax^2 + bx + c \) cho hàm số cụ thể là \( y = x^2 - 6x + 5 \).
Để vẽ đồ thị hàm số này, ta cần xác định một số đặc điểm chính của parabol:
1. **Hàm số dạng chuẩn:** \( y = x^2 - 6x + 5 \)
2. **Tìm đỉnh của parabola:**
- Công thức hoành độ đỉnh: \( x_{đỉnh} = -\frac{b}{2a} \)
- Với \( a=1 \), \( b=-6 \), ta có:
\[
x_{đỉnh} = -\frac{-6}{2 \times 1} = \frac{6}{2} = 3
\]
- Thay \( x=3 \) vào hàm số để tìm y:
\[
y = (3)^2 - 6 \times 3 + 5 = 9 - 18 + 5 = -4
\]
Vậy đỉnh của parabola là điểm \( (3, -4) \).
3. **Tìm các điểm khác để vẽ đồ thị:**
Chọn một số giá trị của \( x \) xung quanh 3 để tính \( y \), ví dụ:
- \( x=2 \):
\[
y= 4 - 12 + 5= -3
\]
- \( x=4 \):
\[
y= 16 - 24 + 5= -3
\]
- \( x=0 \):
\[
y= 0 - 0 + 5= 5
\]
- \( x=5 \):
\[
y= 25 - 30 + 5= 0
\]
4. **Vẽ đồ thị dựa trên các điểm đã tính:**
Các điểm chính: \( (0,5) \), \( (2,-3) \), \( (3,-4) \), \( (4,-3) \), \( (5,0) \)
Bạn có thể dùng các điểm này để vẽ hình parabola y = x^2 - 6x + 5.
Nếu bạn muốn, tôi có thể giúp tạo hình ảnh của đồ thị này. Bạn có muốn tôi giúp vẽ đồ thị không?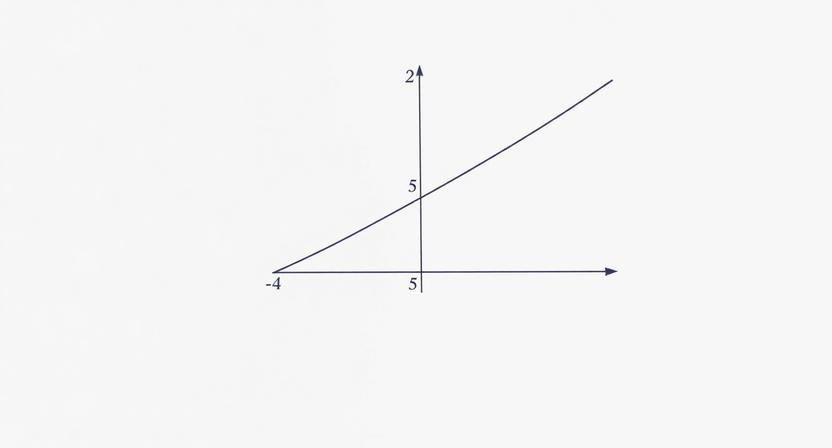
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
89048
Đã trả lời bởi chuyên gia
89048 -
 Đã trả lời bởi chuyên gia
18914
Đã trả lời bởi chuyên gia
18914 -
 Đã trả lời bởi chuyên gia
18730
Đã trả lời bởi chuyên gia
18730 -
 Đã trả lời bởi chuyên gia
14436
Đã trả lời bởi chuyên gia
14436 -
 Đã trả lời bởi chuyên gia
11715
Đã trả lời bởi chuyên gia
11715 -
 Đã trả lời bởi chuyên gia
9702
Đã trả lời bởi chuyên gia
9702