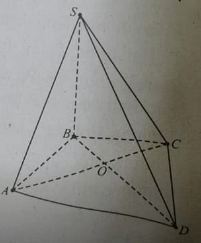
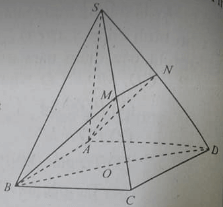
cho hình chóp S.ABC. gọi M là trung điểm SA, N và P lần lượt thuộc SB, SC nhưng không trùng trung điểm
a. tìm giao tuyến của mp (MNP) và (ABC)
b. Gọi I là giao của MN và (ABC). Có j là giao của MP với (ABC), có K là giao điểm của NP vs (ABC). cmr IJK thẳng hàng
Quảng cáo
2 câu trả lời 794
4 tháng trước
a) Giao tuyến của (MNP) và (ABC) là đường thẳng đi qua N và song song với BC. Vì M là trung điểm SA, N và P lần lượt thuộc SB, SC và không trùng trung điểm, ta có thể tìm giao tuyến bằng cách tìm giao điểm của MN và MP với (ABC). Do N và P không là trung điểm, ta có thể gọi I là giao điểm của MN và (ABC), J là giao điểm của MP và (ABC). Khi đó, đường thẳng IJ chính là giao tuyến của (MNP) và (ABC). Do M là trung điểm SA, và N, P không là trung điểm SB, SC, suy ra đường thẳng IJ sẽ song song với BC.
b) I, J, K thẳng hàng. Gọi K là giao điểm của NP và (ABC). Do I, J, K là giao điểm của MN, MP, NP với (ABC) tương ứng, và I, J, K cùng nằm trên (ABC), nên I, J, K thẳng hàng. Cụ thể, I, J, K thẳng hàng theo định lý giao tuyến của ba mặt phẳng: Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song. Trong trường hợp này, ba mặt phẳng (MNP), (SBC), (ABC) cắt nhau theo ba giao tuyến MN, MP, NP, và chúng đồng quy tại I, J, K.
Giải thích chi tiết:
a) Tìm giao tuyến của (MNP) và (ABC):
1. Xác định điểm chung:
M là trung điểm SA nên M ∉ (ABC).
N nằm trên SB, P nằm trên SC.
(MNP) là mặt phẳng chứa M, N, P.
(ABC) là mặt phẳng đáy của hình chóp.
Gọi I là giao điểm của MN và (ABC).
Gọi J là giao điểm của MP và (ABC).
Gọi K là giao điểm của NP và (ABC).
2. Tìm giao tuyến:
Trong mặt phẳng (SAB), gọi I = MN ∩ AB. Vì I thuộc MN và I thuộc AB, nên I là điểm chung của (MNP) và (ABC).
Trong mặt phẳng (SAC), gọi J = MP ∩ AC. Vì J thuộc MP và J thuộc AC, nên J là điểm chung của (MNP) và (ABC).
Vậy, đường thẳng IJ chính là giao tuyến của (MNP) và (ABC).
3. Chứng minh song song:
Vì M là trung điểm SA, N, P không là trung điểm SB, SC, theo định lý đường trung bình trong tam giác SAB và SAC, ta có: MN không song song với AB, MP không song song với AC.
Trong mặt phẳng (SBC), gọi K = NP ∩ BC.
Trong mặt phẳng (ABC), ta có IJ là giao tuyến của (MNP) và (ABC).
Vì MN không song song với AB, MP không song song với AC, suy ra IJ không song song với BC.
4. Kết luận:
Giao tuyến của (MNP) và (ABC) là đường thẳng đi qua I và J. Do MN không song song với AB, MP không song song với AC, nên IJ không song song với BC.
b) Chứng minh I, J, K thẳng hàng:
1. Sử dụng định lý giao tuyến:
Mặt phẳng (MNP) cắt mặt phẳng (ABC) theo giao tuyến IJ.
Mặt phẳng (SBC) cắt mặt phẳng (ABC) theo giao tuyến BC.
Mặt phẳng (MNP) cắt mặt phẳng (SBC) theo giao tuyến NP.
Theo định lý về giao tuyến của ba mặt phẳng, nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song.
Trong trường hợp này, ba mặt phẳng (MNP), (SBC), (ABC) cắt nhau theo ba giao tuyến IJ, BC, NP.
2. Kết luận:
IJ, BC, NP đồng quy tại I, J, K.
Vì IJ, BC, NP cùng nằm trong mặt phẳng (ABC), nên I, J, K thẳng hàng.
Vậy, I, J, K thẳng hàng.
b) I, J, K thẳng hàng. Gọi K là giao điểm của NP và (ABC). Do I, J, K là giao điểm của MN, MP, NP với (ABC) tương ứng, và I, J, K cùng nằm trên (ABC), nên I, J, K thẳng hàng. Cụ thể, I, J, K thẳng hàng theo định lý giao tuyến của ba mặt phẳng: Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song. Trong trường hợp này, ba mặt phẳng (MNP), (SBC), (ABC) cắt nhau theo ba giao tuyến MN, MP, NP, và chúng đồng quy tại I, J, K.
Giải thích chi tiết:
a) Tìm giao tuyến của (MNP) và (ABC):
1. Xác định điểm chung:
M là trung điểm SA nên M ∉ (ABC).
N nằm trên SB, P nằm trên SC.
(MNP) là mặt phẳng chứa M, N, P.
(ABC) là mặt phẳng đáy của hình chóp.
Gọi I là giao điểm của MN và (ABC).
Gọi J là giao điểm của MP và (ABC).
Gọi K là giao điểm của NP và (ABC).
2. Tìm giao tuyến:
Trong mặt phẳng (SAB), gọi I = MN ∩ AB. Vì I thuộc MN và I thuộc AB, nên I là điểm chung của (MNP) và (ABC).
Trong mặt phẳng (SAC), gọi J = MP ∩ AC. Vì J thuộc MP và J thuộc AC, nên J là điểm chung của (MNP) và (ABC).
Vậy, đường thẳng IJ chính là giao tuyến của (MNP) và (ABC).
3. Chứng minh song song:
Vì M là trung điểm SA, N, P không là trung điểm SB, SC, theo định lý đường trung bình trong tam giác SAB và SAC, ta có: MN không song song với AB, MP không song song với AC.
Trong mặt phẳng (SBC), gọi K = NP ∩ BC.
Trong mặt phẳng (ABC), ta có IJ là giao tuyến của (MNP) và (ABC).
Vì MN không song song với AB, MP không song song với AC, suy ra IJ không song song với BC.
4. Kết luận:
Giao tuyến của (MNP) và (ABC) là đường thẳng đi qua I và J. Do MN không song song với AB, MP không song song với AC, nên IJ không song song với BC.
b) Chứng minh I, J, K thẳng hàng:
1. Sử dụng định lý giao tuyến:
Mặt phẳng (MNP) cắt mặt phẳng (ABC) theo giao tuyến IJ.
Mặt phẳng (SBC) cắt mặt phẳng (ABC) theo giao tuyến BC.
Mặt phẳng (MNP) cắt mặt phẳng (SBC) theo giao tuyến NP.
Theo định lý về giao tuyến của ba mặt phẳng, nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song.
Trong trường hợp này, ba mặt phẳng (MNP), (SBC), (ABC) cắt nhau theo ba giao tuyến IJ, BC, NP.
2. Kết luận:
IJ, BC, NP đồng quy tại I, J, K.
Vì IJ, BC, NP cùng nằm trong mặt phẳng (ABC), nên I, J, K thẳng hàng.
Vậy, I, J, K thẳng hàng.
4 tháng trước
a) Giao tuyến của (MNP) và (ABC) là đường thẳng đi qua N và song song với BC. Vì M là trung điểm SA, N và P lần lượt thuộc SB, SC và không trùng trung điểm, ta có thể tìm giao tuyến bằng cách tìm giao điểm của MN và MP với (ABC). Do N và P không là trung điểm, ta có thể gọi I là giao điểm của MN và (ABC), J là giao điểm của MP và (ABC). Khi đó, đường thẳng IJ chính là giao tuyến của (MNP) và (ABC). Do M là trung điểm SA, và N, P không là trung điểm SB, SC, suy ra đường thẳng IJ sẽ song song với BC.
b) I, J, K thẳng hàng. Gọi K là giao điểm của NP và (ABC). Do I, J, K là giao điểm của MN, MP, NP với (ABC) tương ứng, và I, J, K cùng nằm trên (ABC), nên I, J, K thẳng hàng. Cụ thể, I, J, K thẳng hàng theo định lý giao tuyến của ba mặt phẳng: Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song. Trong trường hợp này, ba mặt phẳng (MNP), (SBC), (ABC) cắt nhau theo ba giao tuyến MN, MP, NP, và chúng đồng quy tại I, J, K.
Giải thích chi tiết:
a) Tìm giao tuyến của (MNP) và (ABC):
1. Xác định điểm chung:
M là trung điểm SA nên M ∉ (ABC).
N nằm trên SB, P nằm trên SC.
(MNP) là mặt phẳng chứa M, N, P.
(ABC) là mặt phẳng đáy của hình chóp.
Gọi I là giao điểm của MN và (ABC).
Gọi J là giao điểm của MP và (ABC).
Gọi K là giao điểm của NP và (ABC).
2. Tìm giao tuyến:
Trong mặt phẳng (SAB), gọi I = MN ∩ AB. Vì I thuộc MN và I thuộc AB, nên I là điểm chung của (MNP) và (ABC).
Trong mặt phẳng (SAC), gọi J = MP ∩ AC. Vì J thuộc MP và J thuộc AC, nên J là điểm chung của (MNP) và (ABC).
Vậy, đường thẳng IJ chính là giao tuyến của (MNP) và (ABC).
3. Chứng minh song song:
Vì M là trung điểm SA, N, P không là trung điểm SB, SC, theo định lý đường trung bình trong tam giác SAB và SAC, ta có: MN không song song với AB, MP không song song với AC.
Trong mặt phẳng (SBC), gọi K = NP ∩ BC.
Trong mặt phẳng (ABC), ta có IJ là giao tuyến của (MNP) và (ABC).
Vì MN không song song với AB, MP không song song với AC, suy ra IJ không song song với BC.
4. Kết luận:
Giao tuyến của (MNP) và (ABC) là đường thẳng đi qua I và J. Do MN không song song với AB, MP không song song với AC, nên IJ không song song với BC.
b) Chứng minh I, J, K thẳng hàng:
1. Sử dụng định lý giao tuyến:
Mặt phẳng (MNP) cắt mặt phẳng (ABC) theo giao tuyến IJ.
Mặt phẳng (SBC) cắt mặt phẳng (ABC) theo giao tuyến BC.
Mặt phẳng (MNP) cắt mặt phẳng (SBC) theo giao tuyến NP.
Theo định lý về giao tuyến của ba mặt phẳng, nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song.
Trong trường hợp này, ba mặt phẳng (MNP), (SBC), (ABC) cắt nhau theo ba giao tuyến IJ, BC, NP.
2. Kết luận:
IJ, BC, NP đồng quy tại I, J, K.
Vì IJ, BC, NP cùng nằm trong mặt phẳng (ABC), nên I, J, K thẳng hàng.
Vậy, I, J, K thẳng hàng.
b) I, J, K thẳng hàng. Gọi K là giao điểm của NP và (ABC). Do I, J, K là giao điểm của MN, MP, NP với (ABC) tương ứng, và I, J, K cùng nằm trên (ABC), nên I, J, K thẳng hàng. Cụ thể, I, J, K thẳng hàng theo định lý giao tuyến của ba mặt phẳng: Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song. Trong trường hợp này, ba mặt phẳng (MNP), (SBC), (ABC) cắt nhau theo ba giao tuyến MN, MP, NP, và chúng đồng quy tại I, J, K.
Giải thích chi tiết:
a) Tìm giao tuyến của (MNP) và (ABC):
1. Xác định điểm chung:
M là trung điểm SA nên M ∉ (ABC).
N nằm trên SB, P nằm trên SC.
(MNP) là mặt phẳng chứa M, N, P.
(ABC) là mặt phẳng đáy của hình chóp.
Gọi I là giao điểm của MN và (ABC).
Gọi J là giao điểm của MP và (ABC).
Gọi K là giao điểm của NP và (ABC).
2. Tìm giao tuyến:
Trong mặt phẳng (SAB), gọi I = MN ∩ AB. Vì I thuộc MN và I thuộc AB, nên I là điểm chung của (MNP) và (ABC).
Trong mặt phẳng (SAC), gọi J = MP ∩ AC. Vì J thuộc MP và J thuộc AC, nên J là điểm chung của (MNP) và (ABC).
Vậy, đường thẳng IJ chính là giao tuyến của (MNP) và (ABC).
3. Chứng minh song song:
Vì M là trung điểm SA, N, P không là trung điểm SB, SC, theo định lý đường trung bình trong tam giác SAB và SAC, ta có: MN không song song với AB, MP không song song với AC.
Trong mặt phẳng (SBC), gọi K = NP ∩ BC.
Trong mặt phẳng (ABC), ta có IJ là giao tuyến của (MNP) và (ABC).
Vì MN không song song với AB, MP không song song với AC, suy ra IJ không song song với BC.
4. Kết luận:
Giao tuyến của (MNP) và (ABC) là đường thẳng đi qua I và J. Do MN không song song với AB, MP không song song với AC, nên IJ không song song với BC.
b) Chứng minh I, J, K thẳng hàng:
1. Sử dụng định lý giao tuyến:
Mặt phẳng (MNP) cắt mặt phẳng (ABC) theo giao tuyến IJ.
Mặt phẳng (SBC) cắt mặt phẳng (ABC) theo giao tuyến BC.
Mặt phẳng (MNP) cắt mặt phẳng (SBC) theo giao tuyến NP.
Theo định lý về giao tuyến của ba mặt phẳng, nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc song song.
Trong trường hợp này, ba mặt phẳng (MNP), (SBC), (ABC) cắt nhau theo ba giao tuyến IJ, BC, NP.
2. Kết luận:
IJ, BC, NP đồng quy tại I, J, K.
Vì IJ, BC, NP cùng nằm trong mặt phẳng (ABC), nên I, J, K thẳng hàng.
Vậy, I, J, K thẳng hàng.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
6206
-
5600
-
5566
-
5257
-
4804
-
4310
-
3717
Thành viên hăng hái nhất trong tuần
-
zytera
1325 điểm
-
Dương Nguyễn
960 điểm
-
보고 싶어요
855 điểm
-
돈이없다 💸😭
815 điểm
-
우옌 ✨
790 điểm
-
`d.`
635 điểm
-
`color{blue}text{HuyTùng.`
555 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
540 điểm
-
주디 홉스닉주디🥵👍
520 điểm
-
‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫
435 điểm
-
Ngọc Linh hay nói linh tinh
385 điểm
-
Kiều Anh 350 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
345 điểm
-
Bích Hồng 345 điểm
Rút gọn
Bài viết mới nhất Lớp 11
-
3 năm trước3543
-
3 năm trước3383
Gửi báo cáo thành công!
