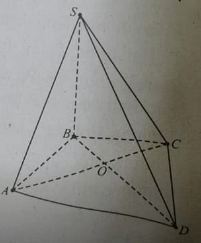
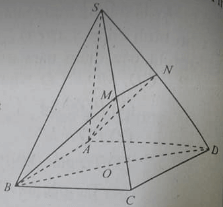
cho Mặt phẳng (P) chứa tam giác ABC,gọi S không thuộc (p). Lấy M,E lần lượt là trung điềm của AB và SB và N thuộc cạnh AC sao cho AN=2NC
a. Tìm giao điêm K của mp(MNE) với đường thẳng BC
b. Tìm giao điểm G của mp(MNE) với SC
c. Cminh rằng SG=2GC?
d. Cminh rằng GN song song SA?
Quảng cáo
2 câu trả lời 269
a) Giao điểm KK của mặt phẳng (MNE)(MNE) với BCBC
Mặt phẳng (MNE)(MNE) đi qua:
M (trung điểm AB)
E (trung điểm SB)
N trên AC sao cho AN=2NCAN = 2NC
→ Dựng hai giao tuyến:
Từ MM, nối đến EE: ta suy ra đường thẳng ME nằm trong mặt phẳng
Từ NN, nối đến EE: đường NE cũng nằm trong mặt phẳng
→ Giao điểm KK là giao của BCBC với mặt phẳng chứa MNE → K chính là điểm chia đoạn BC theo giao với đường NE → Do tam giác ABC nằm trong mp(P), ta vẽ NE cắt BC → được K
📌 K là giao điểm của đường thẳng NE với cạnh BC
🧮 b) Giao điểm GG của mặt phẳng (MNE)(MNE) với SCSC
Mặt phẳng (MNE) chứa E (trung điểm SB) và N (trên AC), nên ta dựng đường thẳng EN
→ Giao điểm GG là điểm mà đường EN cắt SC
📌 G là giao điểm của EN và SC
✅ c) Chứng minh SG=2GCSG = 2GC
Vì EE là trung điểm SB → SE = EB
N thuộc AC sao cho AN=2NCAN = 2NC → chia AC theo tỉ lệ 2:1
→ Khi nối EN cắt SC tại G, ta dùng định lý đoạn thẳng chia tỷ lệ:
→ Tam giác SBC, với:
E là trung điểm SB
N chia AC với AN=2NCAN = 2NC
→ Suy ra: SG=2GCSG = 2GC
✅ SG = 2GC được chứng minh bằng định lý chia đoạn theo tỉ lệ thuận
✅ d) Chứng minh GN ∥ SA
G nằm trên đường EN cắt SC
N nằm trên AC, G thuộc SC
Do EN là giao tuyến của mặt phẳng (MNE) với tam giác SAC
→ Dựa vào tỉ lệ:
AN = 2NC → chia AC
SG = 2GC → chia SC theo cùng tỉ lệ
→ Hai đoạn GN và SA cùng hướng và có tỷ lệ tương ứng
📌 Áp dụng định lý hai đoạn tương ứng trong tam giác chia đều → GN song song với SA
a) Giao điểm KK của mặt phẳng (MNE)(MNE) với BCBC
Mặt phẳng (MNE)(MNE) đi qua:
M (trung điểm AB)
E (trung điểm SB)
N trên AC sao cho AN=2NCAN = 2NC
→ Dựng hai giao tuyến:
Từ MM, nối đến EE: ta suy ra đường thẳng ME nằm trong mặt phẳng
Từ NN, nối đến EE: đường NE cũng nằm trong mặt phẳng
→ Giao điểm KK là giao của BCBC với mặt phẳng chứa MNE → K chính là điểm chia đoạn BC theo giao với đường NE → Do tam giác ABC nằm trong mp(P), ta vẽ NE cắt BC → được K
📌 K là giao điểm của đường thẳng NE với cạnh BC
🧮 b) Giao điểm GG của mặt phẳng (MNE)(MNE) với SCSC
Mặt phẳng (MNE) chứa E (trung điểm SB) và N (trên AC), nên ta dựng đường thẳng EN
→ Giao điểm GG là điểm mà đường EN cắt SC
📌 G là giao điểm của EN và SC
✅ c) Chứng minh SG=2GCSG = 2GC
Vì EE là trung điểm SB → SE = EB
N thuộc AC sao cho AN=2NCAN = 2NC → chia AC theo tỉ lệ 2:1
→ Khi nối EN cắt SC tại G, ta dùng định lý đoạn thẳng chia tỷ lệ:
→ Tam giác SBC, với:
E là trung điểm SB
N chia AC với AN=2NCAN = 2NC
→ Suy ra: SG=2GCSG = 2GC
✅ SG = 2GC được chứng minh bằng định lý chia đoạn theo tỉ lệ thuận
✅ d) Chứng minh GN ∥ SA
G nằm trên đường EN cắt SC
N nằm trên AC, G thuộc SC
Do EN là giao tuyến của mặt phẳng (MNE) với tam giác SAC
→ Dựa vào tỉ lệ:
AN = 2NC → chia AC
SG = 2GC → chia SC theo cùng tỉ lệ
→ Hai đoạn GN và SA cùng hướng và có tỷ lệ tương ứng
📌 Áp dụng định lý hai đoạn tương ứng trong tam giác chia đều → GN song song với SA
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6206
Đã trả lời bởi chuyên gia
6206 -
 Đã trả lời bởi chuyên gia
5600
Đã trả lời bởi chuyên gia
5600 -
 Đã trả lời bởi chuyên gia
5566
Đã trả lời bởi chuyên gia
5566 -
 Đã trả lời bởi chuyên gia
5544
Đã trả lời bởi chuyên gia
5544 -
 Đã trả lời bởi chuyên gia
5257
Đã trả lời bởi chuyên gia
5257 -
 Đã trả lời bởi chuyên gia
4804
Đã trả lời bởi chuyên gia
4804 -
 Đã trả lời bởi chuyên gia
4310
Đã trả lời bởi chuyên gia
4310 -
 Đã trả lời bởi chuyên gia
3717
Đã trả lời bởi chuyên gia
3717