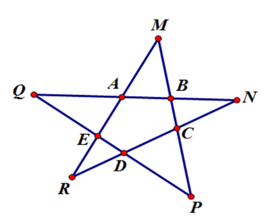
chứng minh hai tia AC,AQ là hai tia đối nhau
Quảng cáo
1 câu trả lời 603
Để chứng minh hai tia \( AC \) và \( AQ \) là hai tia đối nhau, ta cần dựa vào định nghĩa và các tính chất của hai tia đối nhau trong hình học. Hai tia được gọi là đối nhau khi chúng cùng xuất phát từ một điểm và nằm trên cùng một đường thẳng nhưng nằm ở hai hướng khác nhau.
Giả sử và các bước chứng minh:
1. Giả định: Giả sử hai điểm \( A \), \( C \), và \( Q \) thuộc cùng một mặt phẳng, với \( A \) là điểm gốc của hai tia \( AC \) và \( AQ \).
2. Hướng của tia:
- Tia \( AC \) được xác định bởi điểm \( A \) và kéo dài về phía điểm \( C \).
- Tia \( AQ \) được xác định bởi điểm \( A \) và kéo dài về phía điểm \( Q \).
3. Điều kiện để chúng là hai tia đối nhau:
- Ta cần xác định rằng \( A \), \( C \), và \( Q \) thẳng hàng, tức là cả hai điểm \( C \) và \( Q \) nằm trên cùng một đường thẳng đi qua \( A \).
4. Chứng minh thẳng hàng:
- Nếu \( C \) và \( Q \) nằm cùng một đường thẳng với \( A \) nhưng ở hai phía khác nhau, nghĩa là góc \( CAQ \) tạo thành là \( 180^\circ \).
- Điều này có thể chứng minh bằng cách chỉ ra rằng vector \( \overrightarrow{AC} \) và vector \( \overrightarrow{AQ} \) là hai vector ngược chiều nhau, hay nói cách khác, \( \overrightarrow{AC} = -\overrightarrow{AQ} \).
Kết luận
Nếu điểm \( C \) và điểm \( Q \) thỏa mãn điều kiện trên và tạo thành một đường thẳng với điểm \( A \), thì ta có thể kết luận rằng hai tia \( AC \) và \( AQ \) là hai tia đối nhau.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
5325
Đã trả lời bởi chuyên gia
5325 -
 Đã trả lời bởi chuyên gia
2238
Đã trả lời bởi chuyên gia
2238 -
 Đã trả lời bởi chuyên gia
2198
Đã trả lời bởi chuyên gia
2198 -
 Đã trả lời bởi chuyên gia
2189
Đã trả lời bởi chuyên gia
2189

 a; E
a; E