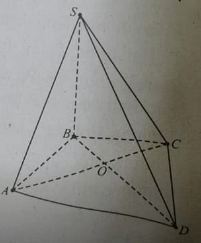
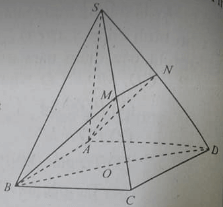
cho hình chóp sabcd có đáy là hình chữ nhật tâm o sa vuông góc vs mp abcd biết a...

Question

cho hình chóp sabcd có đáy là hình chữ nhật tâm o sa vuông góc vs mp abcd biết ab =a ad=3ảng cách từ điểm o đến mặt phẳng sad

VietJack · Accepted Answer

Để xác định khoảng cách từ điểm OOO (tâm của hình chữ nhật ABCDABCDABCD) đến mặt phẳng SADSADSAD, chúng ta sẽ tiến hành theo các bước sau.

Bước 1: Xác định các điểm và tọa độ
Cho hình chóp SABCDSABCDSABCD:

Giả sử chúng ta đặt các điểm trong mặt phẳng tọa độ:A(0,0,0)A(0, 0, 0)A(0,0,0)
B(a,0,0)B(a, 0, 0)B(a,0,0)
C(a,3,0)C(a, 3, 0)C(a,3,0)
D(0,3,0)D(0, 3, 0)D(0,3,0)
S(0,0,h)S(0, 0, h)S(0,0,h) (với hhh là chiều cao của hình chóp).
Tâm của hình chữ nhật OOO được tính là trung điểm của các đỉnh A,B,C,DA, B, C, DA,B,C,D:
O(0+a+a+04,0+0+3+34,0)=O(a2,32,0)O\left(\frac{0 + a + a + 0}{4}, \frac{0 + 0 + 3 + 3}{4}, 0\right) = O\left(\frac{a}{2}, \frac{3}{2}, 0\right)O(40+a+a+0,40+0+3+3,0)=O(2a,23,0)

Bước 2: Phương trình mặt phẳng SADSADSAD
Mặt phẳng SADSADSAD được xác định bởi ba điểm SSS, AAA và DDD. Ta sẽ tìm phương trình của mặt phẳng này bằng cách tính vectơ pháp tuyến của mặt phẳng.

SA→=A−S=(0−0,0−0,0−h)=(0,0,−h)\overrightarrow{SA} = A - S = (0 - 0, 0 - 0, 0 - h) = (0, 0, -h)SA=A−S=(0−0,0−0,0−h)=(0,0,−h)
SD→=D−S=(0−0,3−0,0−h)=(0,3,−h)\overrightarrow{SD} = D - S = (0 - 0, 3 - 0, 0 - h) = (0, 3, -h)SD=D−S=(0−0,3−0,0−h)=(0,3,−h)
Tính tích có hướng của hai vectơ này:
SA→×SD→=∣ijk00−h03−h∣=(0,0,0⋅−h−3⋅−h)−(0⋅−h−0)+(0⋅0−0)=(3h,0,0)\overrightarrow{SA} \times \overrightarrow{SD} = $\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 0 & -h \\ 0 & 3 & -h \end{vmatrix}$ = (0, 0, 0 \cdot -h - 3 \cdot -h) - (0 \cdot -h - 0) + (0 \cdot 0 - 0) = (3h, 0, 0)SA×SD=i00j03k−h−h=(0,0,0⋅−h−3⋅−h)−(0⋅−h−0)+(0⋅0−0)=(3h,0,0)

Vectơ pháp tuyến của mặt phẳng SADSADSAD là (3h,0,0)(3h, 0, 0)(3h,0,0), và do đó phương trình mặt phẳng là:
3hx=d3hx = d3hx=d
Chúng ta có thể đặt d=0d = 0d=0 (do qua điểm S(0,0,h)S(0, 0, h)S(0,0,h)), nên phương trình trở thành:
x=0x = 0x=0

Bước 3: Khoảng cách từ điểm OOO đến mặt phẳng SADSADSAD
Khoảng cách từ một điểm đến mặt phẳng có dạng ax+by+cz+d=0ax + by + cz + d = 0ax+by+cz+d=0 được tính bằng công thức:
Khoảng caˊch=∣ax0+by0+cz0+d∣a2+b2+c2\text{Khoảng cách} = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2 + b^2 + c^2}}Khoảng caˊch=a2+b2+c2∣ax0+by0+cz0+d∣
Áp dụng cho điểm O(a2,32,0)O\left(\frac{a}{2}, \frac{3}{2}, 0\right)O(2a,23,0):

Từ phương trình mặt phẳng 3hx+0y+0z=03hx + 0y + 0z = 03hx+0y+0z=0, ta có a=3h,b=0,c=0,d=0a = 3h, b = 0, c = 0, d = 0a=3h,b=0,c=0,d=0.
Do đó, khoảng cách từ OOO đến mặt phẳng SADSADSAD là:
Khoảng caˊch=∣3h⋅a2+0⋅32+0∣(3h)2+02+02=∣3h⋅a2∣3h=∣a∣2\text{Khoảng cách} = \frac{|3h \cdot \frac{a}{2} + 0 \cdot \frac{3}{2} + 0|}{\sqrt{(3h)^2 + 0^2 + 0^2}} = \frac{|3h \cdot \frac{a}{2}|}{3h} = \frac{|a|}{2}Khoảng caˊch=(3h)2+02+02∣3h⋅2a+0⋅23+0∣=3h∣3h⋅2a∣=2∣a∣
Kết luận
Kết quả là khoảng cách từ điểm OOO đến mặt phẳng SADSADSAD là a2\frac{a}{2}2a.

...Xem thêm

1 câu trả lời 41

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 11