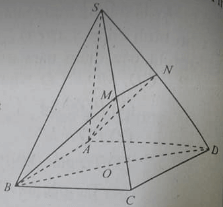
Cho S.ABCD có M,N,P lần lượt thuộc BC,CD,SA.Tìm:
a) AB giao (MNP)
b)SB giao (MNP)
c)SD giao (MNP)
Quảng cáo
1 câu trả lời 180
### Giả sử:
- S.ABCD là một hình chóp, trong đó ABCD là đáy, và S là đỉnh chóp.
- M nằm trên cạnh BC
- N nằm trên cạnh CD
- P nằm trên cạnh SA
### a) Tìm \( AB \cap (MNP) \)
**Mô tả**: Tìm giao điểm giữa đoạn thẳng \( AB \) và mặt phẳng tạo bởi các điểm \( M \), \( N \), và \( P \).
**Cách tiếp cận**:
1. Mặt phẳng \( (MNP) \) được xác định bởi ba điểm không đồng phẳng.
2. Để tìm \( AB \cap (MNP) \), chúng ta cần kiểm tra xem đoạn thẳng \( AB \) có nằm trong mặt phẳng này hay không. Đoạn thẳng \( AB \) nằm trong mặt phẳng nếu có ít nhất một điểm thuộc cả \( AB \) và \( (MNP) \).
### b) Tìm \( SB \cap (MNP) \)
**Mô tả**: Tìm giao điểm giữa đoạn thẳng \( SB \) và mặt phẳng \( (MNP) \).
**Cách tiếp cận**:
1. Tương tự như trên, kiểm tra xem đoạn thẳng \( SB \) có nằm trong mặt phẳng này hay không.
2. Giao điểm \( SB \cap (MNP) \) có thể được xác định bằng cách thay thế vị trí của điểm \( P \) từ đoạn thẳng \( SA \) để xác định vị trí của giao điểm.
### c) Tìm \( SD \cap (MNP) \)
**Mô tả**: Tìm giao điểm giữa đoạn thẳng \( SD \) và mặt phẳng \( (MNP) \).
**Cách tiếp cận**:
1. Phân tích đoạn thẳng \( SD \) để xem có điểm nào trên đoạn này chứa điểm giao nhau của mặt phẳng \( (MNP) \) hay không.
2. Tương tự như các phần trên, kiểm tra vị trí của điểm \( P \) trong khi xét đoạn thẳng \( SD \).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
6206
-
5600
-
5566
-
5257
-
4804
-
4310
-
3717