Ở 1 vùng cứ 15 người thì có 5 người hút thuốc . Biết tỉ lệ người viêm họng trong số người hút thuốc lá là 70 % , trong số nguoi không hút thuốc lá là 20 % . Khám ngẫu nhiên 1 người
.Nếu người này không bị viêm họng thì xác suất người này hút thuốc bằng bao nhiêu ?
Quảng cáo
2 câu trả lời 492
Để giải quyết bài toán này, ta có thể sử dụng định lý Bayes để tính xác suất mong muốn.
Gọi:
- \( A \): Sự kiện người này hút thuốc lá.
- \( B \): Sự kiện người này không bị viêm họng.
Ta cần tìm xác suất của sự kiện \( A \) khi biết sự kiện \( B \) xảy ra, tức là \( P(A|B) \).
Theo định lý Bayes:
\[ P(A|B) = \frac{P(B|A) \times P(A)}{P(B)} \]
Trong đó:
- \( P(B|A) \): Xác suất người này không bị viêm họng khi biết rằng người này hút thuốc lá. Tức là 1 - tỉ lệ người hút thuốc bị viêm họng, \( P(B|A) = 1 - 0.7 = 0.3 \).
- \( P(A) \): Tỉ lệ người hút thuốc lá trong tổng số người, là \( \frac{5}{15} = \frac{1}{3} \).
- \( P(B) \): Xác suất người không bị viêm họng, được tính bằng tổng số người không bị viêm họng trong tổng số người, tức là \( P(B) = \frac{10}{15} = \frac{2}{3} \).
Thay vào công thức, ta có:
\[ P(A|B) = \frac{0.3 \times \frac{1}{3}}{\frac{2}{3}} = \frac{0.3}{2} = 0.15 \]
Vậy, xác suất người này hút thuốc lá khi biết rằng người này không bị viêm họng là \( 0.15 \) hoặc \( 15\% \).
Để giải quyết bài toán này, ta có thể sử dụng định lý Bayes để tính xác suất mong muốn.
Gọi:
- A𝐴: Sự kiện người này hút thuốc lá.
- B𝐵: Sự kiện người này không bị viêm họng.
Ta cần tìm xác suất của sự kiện A𝐴 khi biết sự kiện B𝐵 xảy ra, tức là P(A|B)𝑃(𝐴|𝐵).
Theo định lý Bayes:
P(A|B)=P(B|A)×P(A)P(B)𝑃(𝐴|𝐵)=𝑃(𝐵|𝐴)×𝑃(𝐴)𝑃(𝐵)
Trong đó:
- P(B|A)𝑃(𝐵|𝐴): Xác suất người này không bị viêm họng khi biết rằng người này hút thuốc lá. Tức là 1 - tỉ lệ người hút thuốc bị viêm họng, P(B|A)=1−0.7=0.3𝑃(𝐵|𝐴)=1−0.7=0.3.
- P(A)𝑃(𝐴): Tỉ lệ người hút thuốc lá trong tổng số người, là 515=13515=13.
- P(B)𝑃(𝐵): Xác suất người không bị viêm họng, được tính bằng tổng số người không bị viêm họng trong tổng số người, tức là P(B)=1015=23𝑃(𝐵)=1015=23.
Thay vào công thức, ta có:
P(A|B)=0.3×1323=0.32=0.15𝑃(𝐴|𝐵)=0.3×1323=0.32=0.15
Vậy, xác suất người này hút thuốc lá khi biết rằng người này không bị viêm họng là 0.150.15 hoặc 15%15%.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
11221
Đã trả lời bởi chuyên gia
11221 -
 Đã trả lời bởi chuyên gia
Đã trả lời bởi chuyên gia
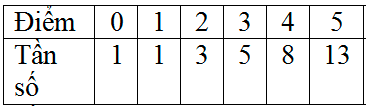
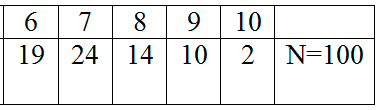
Có 100 học sinh tham dự kì thi HSG Toán (thang điểm 20 điểm) kết quả như sau:
Điểm
9
10
11
12
13
14
Tần số
2
1
2
10
8
8
Điểm
15
16
17
18
19
Cộng
Tần số
24
18
14
10
3
100
Tính độ lệch chuẩn (kết quả làm tròn đến hai chữ số thập phân).
A. 4,67
B. 2,16
C. 4,70
D. 2,17
10106 -
 Đã trả lời bởi chuyên gia
7225
Đã trả lời bởi chuyên gia
7225 -
 Đã trả lời bởi chuyên gia
6785
Đã trả lời bởi chuyên gia
6785 -
 Đã trả lời bởi chuyên gia
Đã trả lời bởi chuyên gia
Một xạ thủ bắn 30 viên đạn vào bia kết quả được ghi lại trong bảng phân bổ tần số sau:
Lớp
Tần số
6
7
8
9
10
4
3
8
9
6
Cộng
30
Khi đó điểm số trung bình cộng là (kết quả làm tròn đến hàng phần trăm):
A. 8,33
B. 8,34
C. 8,31
D. 8,32
6011 -
 Đã trả lời bởi chuyên gia
Đã trả lời bởi chuyên gia
Hai lớp 10C, 10D của một trường Trung học phổ thông đồng thời làm bài thi môn Ngữ văn theo cùng một đề thi. Kết quả thi được trình bày ở hai bảng phân bố tần số sau đây:
Điểm thi Ngữ văn của lớp 10C
Điểm thi 5 6 7 8 9 10 Cộng Tần số 3 7 12 14 3 1 40 Điểm thi Ngữ văn của lớp 10D
Điểm thi 6 7 8 9 Cộng Tần số 8 18 10 4 40 a) Tính các số trung bình, phương sai, độ lệch chuẩn của các bảng phân bố đã cho.
b) Xét xem kết quả làm bài thi của môn Ngữ văn ở lớp nào là đều hơn.
5171 -
 Đã trả lời bởi chuyên gia
4879
Đã trả lời bởi chuyên gia
4879 -
 Đã trả lời bởi chuyên gia
4135
Đã trả lời bởi chuyên gia
4135