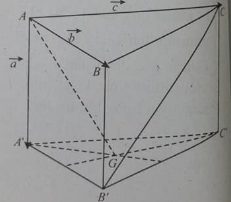
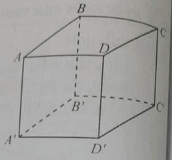
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính khoảng cách giữa hai đường thẳng B'C và A'B
Quảng cáo
1 câu trả lời 326
Để tính khoảng cách giữa hai đường thẳng B'C và A'B trong hình lập phương ABCD.A'B'C'D', ta sẽ sử dụng hình học không gian.
Đường thẳng B'C và A'B là hai cạnh của mặt phẳng vuông góc với mặt phẳng (ABCD) và qua tâm của hình lập phương.
Ta có thể giả sử điểm O là tâm của hình lập phương và đồng thời là giao điểm của đường thẳng B'C và A'B.
Khoảng cách giữa hai đường thẳng này chính là khoảng cách từ điểm O đến mặt phẳng (B'C).
Khoảng cách từ một điểm đến một mặt phẳng có thể được tính bằng công thức:
\[ d = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2 + b^2 + c^2}} \]
Trong đó (a, b, c) là vector pháp tuyến của mặt phẳng, (x₀, y₀, z₀) là tọa độ của điểm, và d là hằng số.
Trong trường hợp này, vector pháp tuyến của mặt phẳng (B'C) là \(\vec{n_{B'C}} = \vec{BC} \times \vec{BC'}\) và vector pháp tuyến của mặt phẳng (A'B) là \(\vec{n_{A'B}} = \vec{AB} \times \vec{A'B'}\).
Sau đó, ta có thể tính khoảng cách từ tâm O đến mặt phẳng (B'C) và (A'B) bằng cách sử dụng công thức trên.
Cuối cùng, khoảng cách giữa hai đường thẳng B'C và A'B sẽ là hiệu giữa hai khoảng cách này.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
14684
Đã trả lời bởi chuyên gia
14684 -
 Đã trả lời bởi chuyên gia
14438
Đã trả lời bởi chuyên gia
14438 -
 Đã trả lời bởi chuyên gia
11758
Đã trả lời bởi chuyên gia
11758 -
 Đã trả lời bởi chuyên gia
11104
Đã trả lời bởi chuyên gia
11104