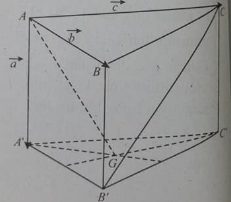
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông với AB = AC = a, góc giữa BC' và ( ABC ) bằng 45\deg . Tính thể tích khối lăng trụ.
Quảng cáo
1 câu trả lời 407
Để tính thể tích của khối lăng trụ, ta cần biết diện tích đáy và chiều cao của lăng trụ.
1. **Diện tích đáy của lăng trụ:**
Vì tam giác \(ABC\) là tam giác vuông, diện tích của nó có thể tính bằng công thức \(S_{ABC} = \frac{1}{2} \times AB \times AC = \frac{1}{2} \times a \times a = \frac{a^2}{2}\).
2. **Chiều cao của lăng trụ:**
Chiều cao của lăng trụ chính là đoạn thẳng \(AA'\), nằm trên đoạn thẳng \(BC\). Ta cần tìm chiều dài của đoạn thẳng này.
Vì góc giữa \(BC'\) và mặt phẳng chứa tam giác \(ABC\) là \(45^\circ\), nên ta có thể sử dụng tỉ lệ giữa độ dài các cạnh của hai tam giác \(ABC'\) và \(ABC\).
Theo đề bài, ta có \(AB = AC = a\), nên \(ABC\) là tam giác cân.
Do đó, \(BC'\) sẽ là đường cao của tam giác \(ABC'\), và theo định lý cạnh bên của tam giác vuông, \(BC' = \frac{AB}{\sqrt{2}} = \frac{a}{\sqrt{2}}\).
Đồng thời, \(AA'\) sẽ là đường cao của tam giác \(ABC\), nên \(AA' = BC' = \frac{a}{\sqrt{2}}\).
3. **Thể tích của lăng trụ:**
Thể tích \(V\) của lăng trụ được tính bằng tích diện tích đáy \(S_{ABC}\) với chiều cao \(AA'\):
\[V = S_{ABC} \times AA' = \frac{a^2}{2} \times \frac{a}{\sqrt{2}} = \frac{a^3}{2\sqrt{2}}.\]
Vậy, thể tích của khối lăng trụ là \(V = \frac{a^3}{2\sqrt{2}}\).
Quảng cáo
Bạn muốn hỏi bài tập?