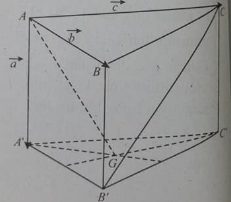
Cho hình thoi S.ABCD, đáy ABCD là hình thoi tâm O cạnh a, cạnh bên SA vuông góc với mp đáy, SA=. Góc ABC=60°
a) Chứng minh (SBD) góc với (SAC)
b) Tìm góc giữa 2 mp(SBD) và (ABCD)
c) Gọi M,N lần lượt là trung điểm BC,CD Tìm góc giữa 2 mp(SBD) và (SMN)
Quảng cáo
1 câu trả lời 184
a) Ta có:
- Tam giác SAC vuông tại S, góc A bằng 60 độ
- Góc SAB bằng 180 - 60 = 120 độ
- Hai tam giác SAC và SAB cân tại SA
Do đó:
- Góc (SBD) bằng 60 độ + (góc DBC) = 60 độ + (góc ABC)/2 = 60 độ + 30 độ = 90 độ - (góc BAS)
- Góc (SAC) bằng 90 độ - (góc BAS)
Vậy (SBD) góc với (SAC).
b) Gọi E là trung điểm AB, ta có BE cùng phân giác góc ABC nên góc CEB = 30 độ. Vì hình thoi ABCD nên AE song song với DB. Khi đó, ta có:
- Góc AED = 180 độ - góc DAC - góc ADB = 180 độ - 60 độ - 60 độ = 60 độ
- SP song song với DE, nên góc (SBD) bằng góc ESQ, trong đó Q là giao điểm của SA và DE
- Từ tam giác đều ASE, ta có góc SQE = 60 độ
Do đó, góc giữa hai mp (SBD) và (ABCD) bằng 60 độ + 60 độ = 120 độ.
c) Ta có:
- S là trung điểm AD
- M,N lần lượt là trung điểm BC,CD nên MN song song với AB
Khi đó, ta có:
- Góc (SMN) bằng góc (SNM) = (góc ANS) - (góc BNM)
- Góc ANS bằng 90 độ - (góc NAS), trong đó NS vuông góc với AB tại S
- Góc BNM bằng góc BMQ
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
14687
Đã trả lời bởi chuyên gia
14687 -
 Đã trả lời bởi chuyên gia
14453
Đã trả lời bởi chuyên gia
14453 -
 Đã trả lời bởi chuyên gia
11763
Đã trả lời bởi chuyên gia
11763 -
 Đã trả lời bởi chuyên gia
11113
Đã trả lời bởi chuyên gia
11113