Question

Đã trả lời bởi chuyên gia

Answer 1

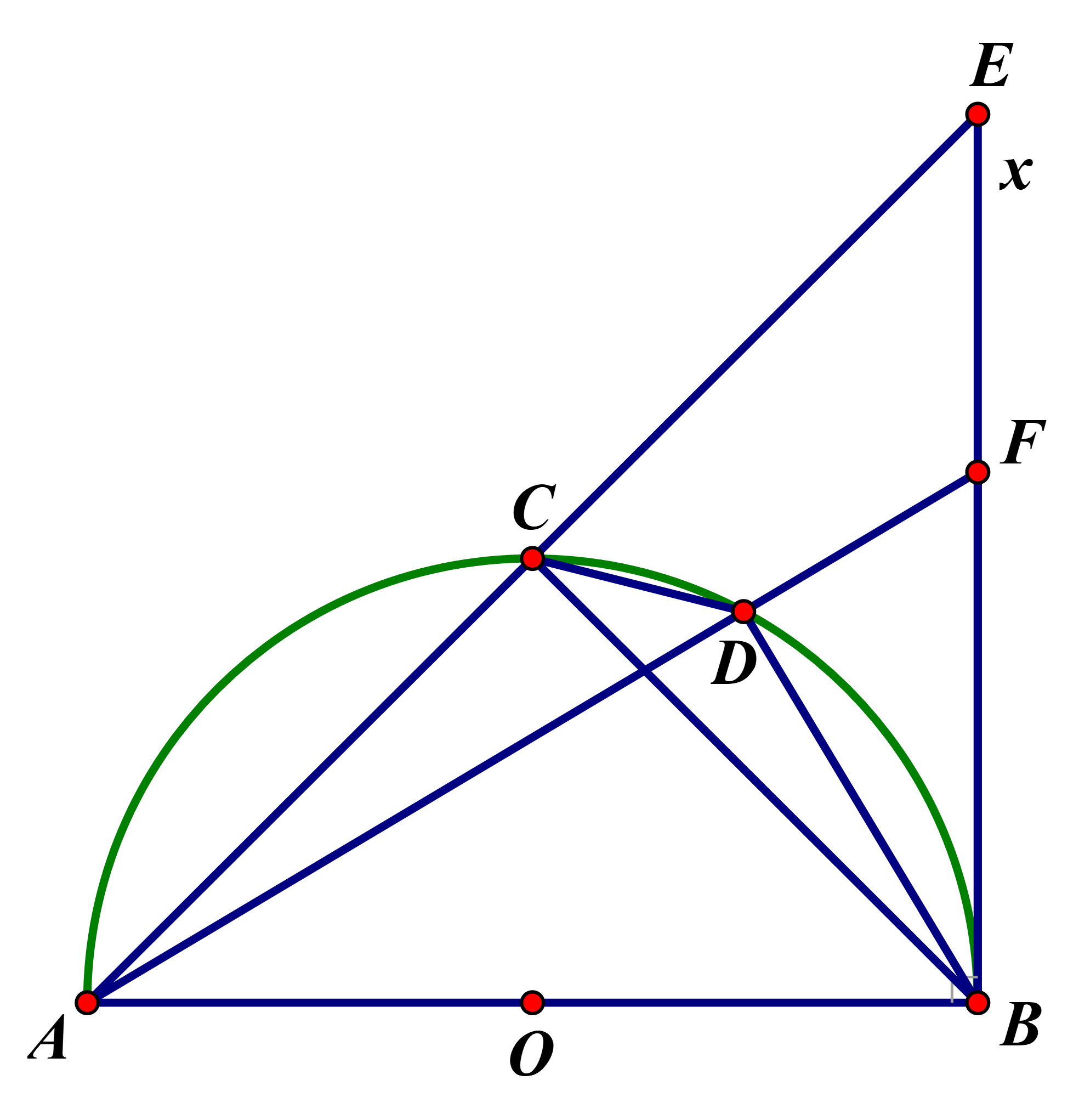
a.

Ta có góc CAB= góc CBA(hai góc nội tiếp chắn hai cung bằng nhau)

Ta lại có: góc ACB= 90° (góc nội tiếp chắn nửa đường tròn)

=> tam giác CAB là tam giác vuông cân và góc CAB= 45°

Xét tam giác ABE vuông tại B (Bx là tiếp tuyến của (O)) có góc EAB= 45°

Dẫn đến góc AEB = 180° −góc ABE− góc EAB= 180 – 90 – 45 = 45° = góc EAB

Suy ra tam giác ABE là tam giác vuông cân.

b.
Xét ∆ FDB và ∆ FBA có:

Góc AFBlà góc chung
góc FBA= góc ADB = 90° (góc ADB là góc nội tiếp chắn nữa đường tròn và Bx là tiếp tuyến của (O))

Suy ra ∆ FDB ~ ∆ FBA (g.g)

Từ đó suy ra

FB/FA=FD/FB

⇔ FB^2 = FD.FA (đpcm)

c.
Từ câu b ta suy ra được: Trong một tam giác vuông thì bình phương cạnh góc vuông bằng tích hình chiếu của nó trên cạnh huyền nhân với cạnh huyền.

Xét tam giác ABF vuông tại B đường cao BD ta có: AB^2 = AD.AF

ABE vuông tại B đường cao BC ta có:
AB^2 = AC.AE

Suy ra AD.AF = AC.AE (đpcm)

...Xem thêm

Answer 2

a.