Văn Long
Đồng đoàn
250
50
Cho hàm số y=13x4−143x2 có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M(x1;y1),N(x2;y2) (M, N khác A) thỏa mãn ?
A.2
B.1
C.3
D.0
Trong không gian Oxyz, cho hai mặt phẳng (P):x−y+2z+1=0 , (Q):2x+y+z−1=0 . Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ đúng một mặt cầu (S) thỏa yêu cầu.
A.√3
B.√22
C.√62
D.3√22
Cho hai số thực x, y thỏa mãn điều kiện x≠0,−1≤y≤132 và 4x2+1x2−1=log2[14−(y−2)√y+1] . Giá trị của x2−2xy+3y2+1 bằng
A.4
B.2
C.-4
D-2
Cho lăng trụ tam giác đều ABC.A'B'C' cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng (P) qua B' và vuông góc A'C chia lăng trụ thành hai khối. Biết thể tích của hai khối lần lượt là V1, V2 với V1 < V2. Tỉ số V1V2 gần giá trị nào sau đây nhất?
A.0.045
B.0.03
C.0.21
D.0.16
Cho hai đường tròn (O1;5) và (O2;3) cắt nhau tại 2 điểm A, B sao cho AB là một đường kính của đường tròn (O2) . Gọi (D) là hình phẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần tô màu như hình vẽ). Quay (D) quanh trục O1O2 ta được 1 khối tròn xoay. Tính thể tích khối tròn xoay được tạo thành.
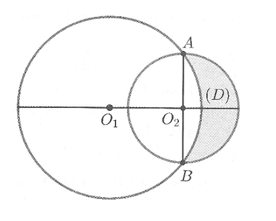
A.36π
B.68π3
C.14π3
D.40π3
Cho hàm số f(x) có đồ thị của hàm số f’(x) như sau:

Hàm số y=f(2x−1)+x33+x2−2x nghịch biến trên khoảng nào sau đây?
A.(-1;0)
B.(-6;-3)
C.(3;6)
D.(6;+∞)
Cho hàm số y=x+1x−1 có đồ thị (C). Giả sử A, B là hai điểm thuộc (C) và đối xứng với nhau qua giao điểm của hai đường tiệm cận. Dựng hình vuông AEBF. Diện tích nhỏ nhất của hình vuông AEBF là?
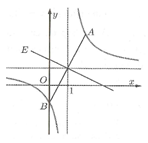
A.8√2
B.4√2
C.8
D.16
Có bao nhiêu giá trị nguyên của tham số m thuộc[−10;10] để phương trình log5(mx)log5(x+1)=2 có nghiệm duy nhất?
A.9
B.vô số
C.10
D.15
Cho số phức z=a+bi(a,b∈ℝ,a<0) thỏa mãn điều kiện 1+ˉz=|ˉz−i|2+(iz−1)2 . Tính |z|
A.√22
B.√5
C.√172
D.12
Trong không gian Oxyz, cho ba mặt phẳng (P):x−2y+z−1=0;(Q):x−2y+z+8=0,(R):x−2y+z−4=0
Một đường thẳng d thay đổi cắt ba mặt phẳng (P), (Q), (R) lần lượt tại A, B, C. Giá trị nhỏ nhất của T=AB2+144AC bằng
A.723√3
B.96
C.108
D.32
Gọi S là tập hợp các số tự nhiên gồm 9 chữ số khác nhau. Chọn ngẫu nhiên một số từ S, tính xác suất để chọn được một số gồm 4 chữ số lẻ và chữ số 0 luôn đứng giữa hai chữ số lẻ (hai số hai bên chữ số 0 là số lẻ).
A.4954
B.554
C.17776
D.4554
Cho hàm số y = f (x) có đồ thị (C) như hình vẽ dưới đây. Số nghiệm của phương trình f[f(x)]=0 là
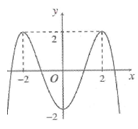
A.6
B.12
C.8
D.10
Cho 1∫0x3+2x2+3x+2dx=1a+b.ln32 với với a, b là các số thực dương. Có bao nhiêu giá trị nguyên của k để 5ab∫8dx>limx→+∞(k2+1).x+2017x+2018 ?
A.5
B.3
C.vô số
D.7
Cho số phức z=x+yi(x,y∈ℝ) thỏa mãn |z−i|=|ˉz−2−3i| và |z| đạt giá trị nhỏ nhất. Giá trị của 3x−y bằng
A.-6
B.−83
C.43
D.3
Cho hàm số y = f(x) có đồ thị đạo hàm f’(x) như sau: 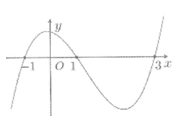
Gọi S là tập hợp tất các giá trị nguyên m∈[−5;5] để hàm số g(x) = f(x + m) nghịch biến trên (1; 2). Hỏi tập S có tất cả bao nhiêu phần tử?
A.5
B.7
C.vô số
D.2
Trong không gian Oxyz, cho mặt phẳng (P):x+2y+3z−6=0 và đường thẳng d:x+12=y+23=z+12 . Phương trình đường thẳng d' là hình chiếu vuông góc của d lên (P) là:
A.d':x−11=y−11=z−11
B.d':x+11=y+11=z−3−1
C.d':x−11=y1=z−2−1
D.d':x−1=y2=z−2−1
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. AB=a,AC=a√3. Tam giác SBC đều và nằm trong mặt phẳng vuông với đáy (tham khảo hình vẽ bên). Tính khoảng cách từ điểm B đến mặt phẳng (SAC).
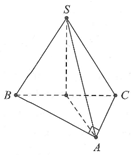
A.√39a13
B.√6a2
C.√3a2
D.2√39a13
Biết F(x)=(ax2+bx+c).ex là một nguyên hàm của hàm số f(x)=(x2+5x+5).ex . Giá trị của 2a+3b+c bằng
A.6
B.13
C.8
D.10
Để tính diện tích xung quanh của một khối cầu bằng đá, người ta thả nó vào trong một chiếc thùng hình trụ có chiều cao 2m bán kính đường tròn đáy bằng 0,5m và chứa một lượng nước có thể tích bằng 18 thể tích khối trụ. Sau khi thả khối cầu bằng đá vào khối trụ người ta đo được mực nước trong khối trụ cao gấp ba lần mực nước ban đầu khi chưa thả khối cầu. Diện tích xung quanh của khối cầu gần bằng kết quả nào được cho dưới đây?
A.2,6m2
B.1,1m2
C.3,4m2
D.1,7m2


