Đường

x³−5x²=x²(x−5)

Mol (ký hiệu: mol) là đơn vị đo lường cơ bản trong hệ SI (Hệ đo lường quốc tế), dùng để định lượng chất dựa trên số lượng các hạt vi mô (như nguyên tử, phân tử, ion, electron,...) có trong một mẫu vật.

1. Định nghĩa khoa học
1 mol chứa 6.02214076 × 10²³ hạt (số Avogadro - NANA​).

Ví dụ:

1 mol nguyên tử Carbon (C) = 6.022×10236.022×10^23 nguyên tử C.
1 mol phân tử nước (H₂O) = 6.022×10236.022×10^23 phân tử H₂O.

mm: khối lượng chất (gam).
MM: khối lượng mol (gam/mol).
VV: thể tích khí (lít).
NN: số hạt vi mô.
(đktc: điều kiện tiêu chuẩn, 0°C và 1 atm)*

Giả thiết:
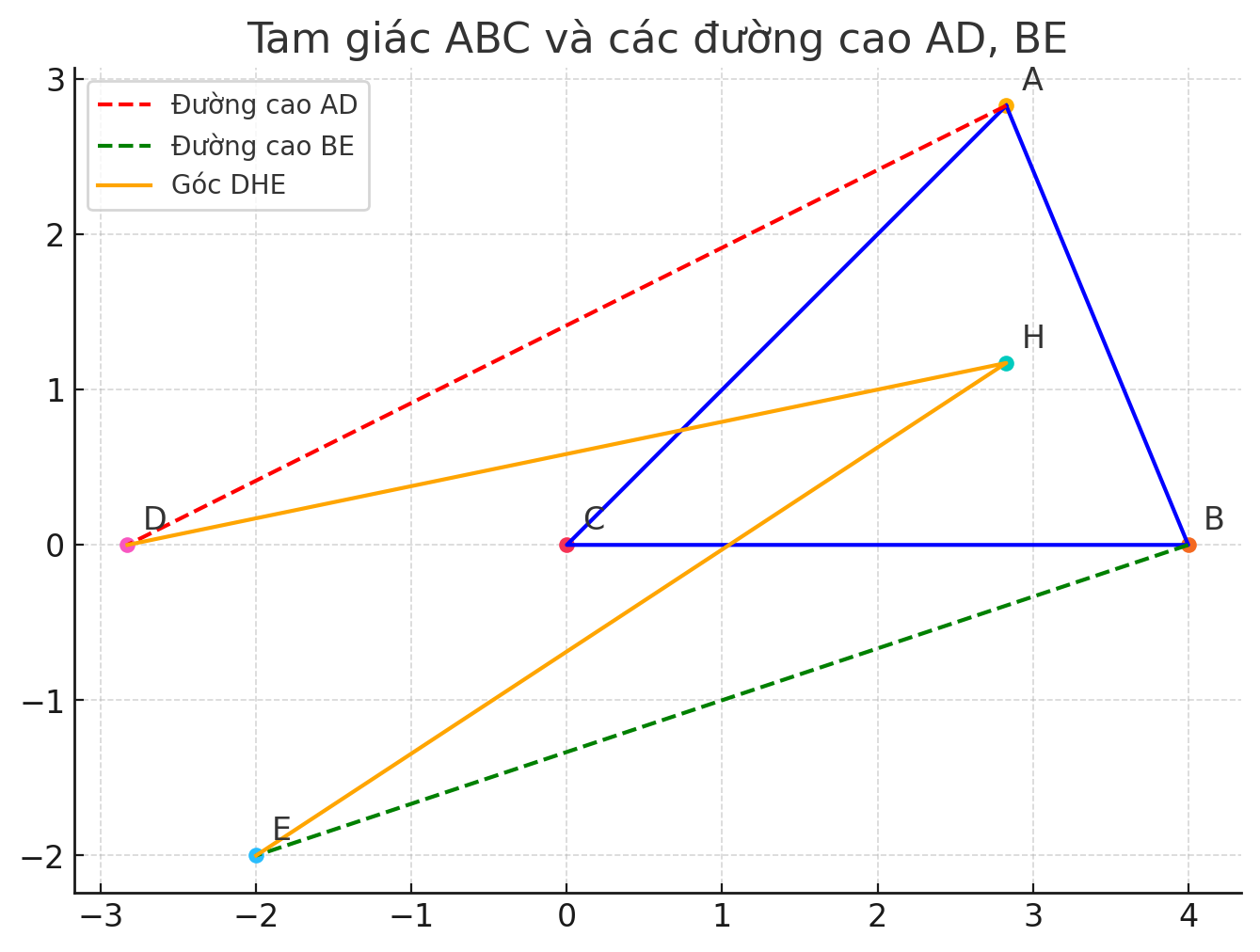
Tam giác ABCABCABC nhọn, ∠ACB=45∘\angle ACB = 45^\circ∠ACB=45∘
Đường cao ADADAD và BEBEBE cắt nhau tại HHH (trong đó D∈BCD \in BCD∈BC, E∈ACE \in ACE∈AC, AD⊥BCAD \perp BCAD⊥BC, BE⊥ACBE \perp ACBE⊥AC)

a. Tính góc ∠DHE\angle DHE∠DHE:
Do AD⊥BCAD \perp BCAD⊥BC và BE⊥ACBE \perp ACBE⊥AC, nên HHH là trực tâm của tam giác ABCABCABC.

Góc ∠DHE\angle DHE∠DHE là góc giữa hai đường cao cắt nhau tại trực tâm. Trong tam giác nhọn:

∠DHE=180∘−∠C\angle DHE = 180^\circ - \angle C∠DHE=180∘−∠CVì ∠C=∠ACB=45∘\angle C = \angle ACB = 45^\circ∠C=∠ACB=45∘, nên:

∠DHE=135∘\boxed{\angle DHE = 135^\circ}∠DHE=135∘​
b. Chứng minh tam giác △CDA∼△CEB\triangle CDA \sim \triangle CEB△CDA∼△CEB (g.g):
Xét hai tam giác CDACDACDA và CEBCEBCEB:

∠CAD=∠CBE=90∘\angle CAD = \angle CBE = 90^\circ∠CAD=∠CBE=90∘ (do là các đường cao)
∠ACD=∠BCE\angle ACD = \angle BCE∠ACD=∠BCE (cùng là góc tại đỉnh CCC)
→ Tam giác CDA∼CEBCDA \sim CEBCDA∼CEB theo trường hợp g.g (góc-góc).

△CDA∼△CEB (g.g)\boxed{\triangle CDA \sim \triangle CEB \ (\text{g.g})}△CDA∼△CEB (g.g)​
c. Chứng minh tam giác CDE∼CABCDE \sim CABCDE∼CAB:
Xét hai tam giác CDECDECDE và CABCABCAB:

∠DEC=90∘\angle DEC = 90^\circ∠DEC=90∘ (do BE⊥ACBE \perp ACBE⊥AC)
∠DCE=90∘\angle DCE = 90^\circ∠DCE=90∘ (do AD⊥BCAD \perp BCAD⊥BC)
Tam giác CDECDECDE vuông tại cả hai điểm? Điều này sẽ không hợp lý. Nhưng nếu D∈BCD \in BCD∈BC, E∈ACE \in ACE∈AC, và tam giác CDECDECDE là phần trong tam giác lớn CABCABCAB, ta cần chứng minh đồng dạng theo một cách khác.

Nhưng! Từ việc tam giác CDA∼CEBCDA \sim CEBCDA∼CEB ở trên (b), và nếu chúng ta kết hợp tam giác CDECDECDE, có thể suy ra:

Tam giác CDE∼CABCDE \sim CABCDE∼CAB nếu như các góc tương ứng bằng nhau.
Ví dụ:

∠CDE=∠CAB\angle CDE = \angle CAB∠CDE=∠CAB
∠DCE=∠CBA\angle DCE = \angle CBA∠DCE=∠CBA
=> Nếu chứng minh được hai cặp góc đó bằng nhau → Tam giác đồng dạng theo g.g.

Nếu giả thiết có thêm rằng D∈BCD \in BCD∈BC, E∈ACE \in ACE∈AC, và hai điểm này là chân đường cao thì ta có thể thiết lập:

△CDE∼△CAB\boxed{\triangle CDE \sim \triangle CAB}△CDE∼△CAB​
d. Diện tích tam giác CDECDECDE bằng diện tích tam giác ADBEADBEADBE:
Xét:

Tam giác ADBEADBEADBE gồm 2 tam giác vuông nhỏ là ABDABDABD và ABEABEABE
Tam giác CDECDECDE cũng nằm trong hình gồm các đường cao giao nhau tại trực tâm
Từ giả thiết các tam giác đồng dạng, nếu:

△CDE∼△CAB\triangle CDE \sim \triangle CAB△CDE∼△CAB
Và các tỉ số cạnh đảm bảo
Có thể diện tích các tam giác nhỏ là bằng nhau nhờ tính chất đồng dạng và sự đối xứng từ trực tâm.

Vì vậy:

SCDE=SADBE\boxed{S_{CDE} = S_{ADBE}}SCDE​=SADBE​​

Đường màu xanh là đồ thị của hàm số.
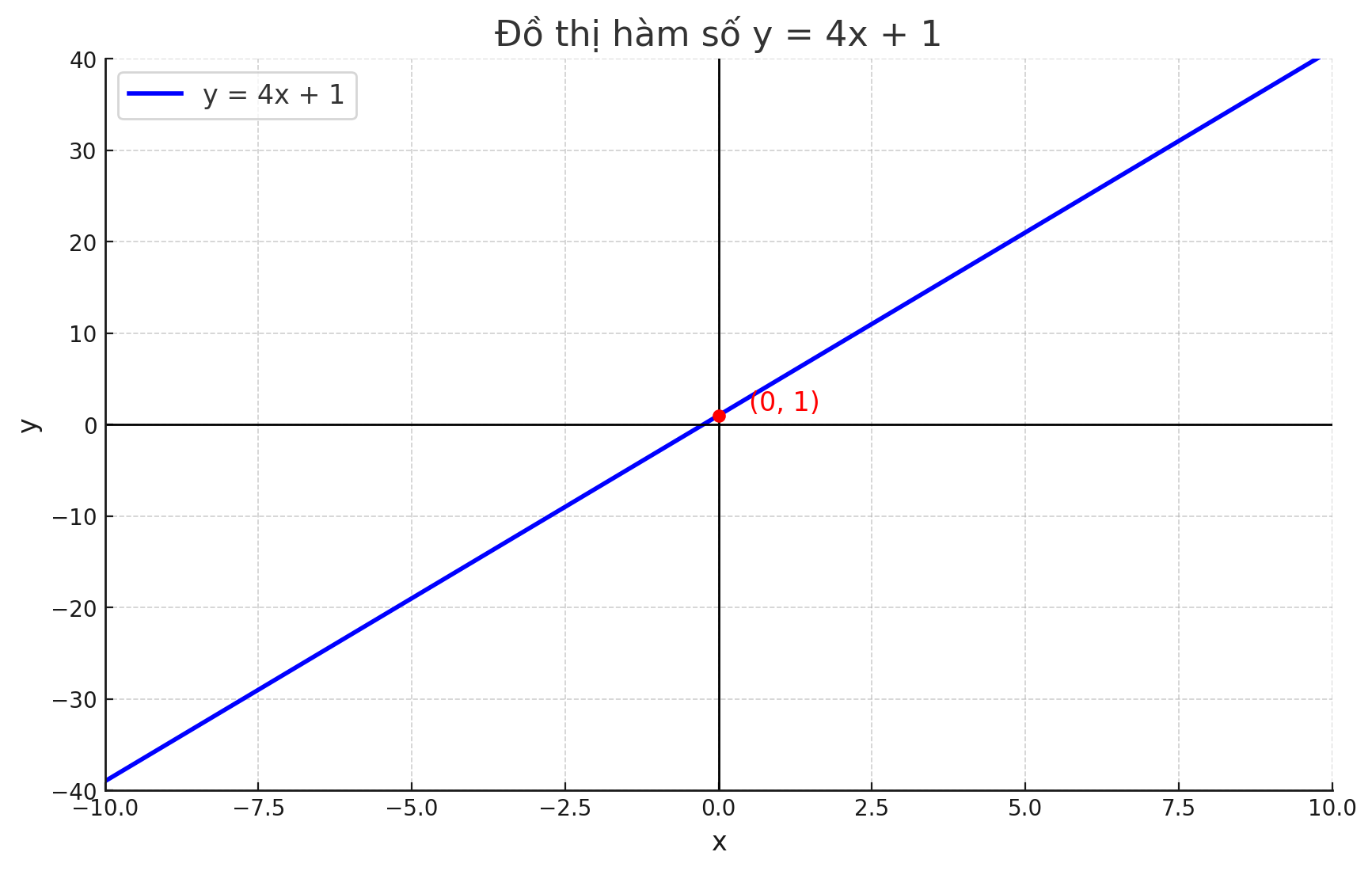
Điểm màu đỏ là giao điểm với trục tung tại (0,1)(0, 1)(0,1).
Có trục tọa độ và lưới rõ ràng để dễ đọc giá trị.
Nếu bạn cần thêm điểm đặc biệt khác, vẽ giao điểm với trục hoành, hay muốn đổi màu, mình làm tiếp cho nhé! ​