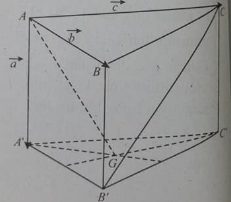
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với (ABCD). Gọi là góc giữa BD và (SAD). Tính sin
A. sin =
B. sin =
C. sin =
D. sin =
Quảng cáo
1 câu trả lời 874
5 năm trước
Đáp án A
Gọi N là trung điểm AD suy ra HN // BD.
Góc giữa BD và (SAD) bằng góc giữa HN và (SAD).
Ta có AD⊥SH, AD⊥AB suy ra AD⊥ (SAB) . Trong mặt phẳng (SAB) kẻ HK⊥SA nên ta suy ra AD⊥HK và HK⊥ (SAD) . vậy góc giữa HN và (SAD) là góc HNK.
Gọi cạnh của hình vuông là a
Ta tính được HN = . Xét tam giác vuông SHA vuông tại H ta có
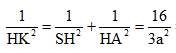
![]()
Xét tam giác vuông HNK vuông tại K ta có ![]()
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
Gửi báo cáo thành công!