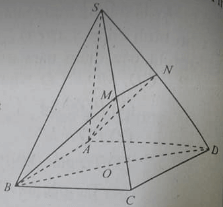
Cho hình chóp S.ABCD có đáy là hình bình hành . Gọi Q là trung điểm DC. G là trọng tâm tam giác SCD. Điểm N thuộc đoạn thẳng AC sao cho NG// (SAB) . Tính NC/NA
Quảng cáo
1 câu trả lời 97
Để tính tỉ lệ
NC/NAcap N cap C / cap N cap A
𝑁𝐶/𝑁𝐴
, ta sử dụng tính chất đường song song và trọng tâm tam giác: Gcap G
𝐺
là trọng tâm △SCDtriangle cap S cap C cap D
△𝑆𝐶𝐷
, Qcap Q
𝑄
trung điểm DCcap D cap C
𝐷𝐶
, Gcap G
𝐺
nằm trên SQcap S cap Q
𝑆𝑄
và SG=2GQcap S cap G equals 2 cap G cap Q
𝑆𝐺=2𝐺𝑄
. Vì NG//(SAB)cap N cap G / / open paren cap S cap A cap B close paren
𝑁𝐺//(𝑆𝐴𝐵)
, ta tìm giao tuyến của NGcap N cap G
𝑁𝐺
với các mặt phẳng chứa SABcap S cap A cap B
𝑆𝐴𝐵
và áp dụng định lý <>Thales trong △SACtriangle cap S cap A cap C
△𝑆𝐴𝐶
, hoặc xét mặt phẳng (SQM)open paren cap S cap Q cap M close paren
(𝑆𝑄𝑀)
(với Mcap M
𝑀
là giao điểm của SQcap S cap Q
𝑆𝑄
với mặt phẳng (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
), từ đó suy ra NC/NA=1/2cap N cap C / cap N cap A equals 1 / 2
𝑁𝐶/𝑁𝐴=1/2
hoặc 2/12 / 1
2/1
tùy cách xác định (thực tế, NC/NA=2/1cap N cap C / cap N cap A equals 2 / 1
𝑁𝐶/𝑁𝐴=2/1
do Gcap G
𝐺
nằm ngoài đoạn SQcap S cap Q
𝑆𝑄
).
Các bước giải chi tiết:
Xác định vị trí điểm G và đường thẳng SQ: Gcap G
𝐺
là trọng tâm tam giác SCDcap S cap C cap D
𝑆𝐶𝐷
, Qcap Q
𝑄
là trung điểm DCcap D cap C
𝐷𝐶
. Gcap G
𝐺
nằm trên đoạn SQcap S cap Q
𝑆𝑄
và SG=2GQcap S cap G equals 2 cap G cap Q
𝑆𝐺=2𝐺𝑄
(tức là SQ=SG+GQ=3GQcap S cap Q equals cap S cap G plus cap G cap Q equals 3 cap G cap Q
𝑆𝑄=𝑆𝐺+𝐺𝑄=3𝐺𝑄
).
Tìm mặt phẳng chứa đường thẳng (SAB) và cắt NG:Ta có NG//(SAB)cap N cap G / / open paren cap S cap A cap B close paren
𝑁𝐺//(𝑆𝐴𝐵)
.
Mặt phẳng (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
chứa SAcap S cap A
𝑆𝐴
và SBcap S cap B
𝑆𝐵
.
Xét mặt phẳng (SAC)open paren cap S cap A cap C close paren
(𝑆𝐴𝐶)
chứa ACcap A cap C
𝐴𝐶
và SAcap S cap A
𝑆𝐴
.
Xét mặt phẳng (SQM)open paren cap S cap Q cap M close paren
(𝑆𝑄𝑀)
(mặt phẳng đi qua S,Qcap S comma cap Q
𝑆,𝑄
và song song hoặc cắt (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
).
Sử dụng định lý Thales (hoặc định lý Menelaus):Vì NG//(SAB)cap N cap G / / open paren cap S cap A cap B close paren
𝑁𝐺//(𝑆𝐴𝐵)
, nên đường thẳng NGcap N cap G
𝑁𝐺
cắt mặt phẳng (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
tại một điểm Kcap K
𝐾
(hoặc NGcap N cap G
𝑁𝐺
song song với (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
và ta cần tìm một mặt phẳng khác).
Xét mặt phẳng (SAC)open paren cap S cap A cap C close paren
(𝑆𝐴𝐶)
. Gọi Mcap M
𝑀
là giao điểm của SQcap S cap Q
𝑆𝑄
với mặt phẳng (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
. (Cách này hơi phức tạp).
Cách 2 (Dùng mặt phẳng chứa NG và giao tuyến):Kẻ QM′cap Q cap M prime
𝑄𝑀′
// SAcap S cap A
𝑆𝐴
( M′cap M prime
𝑀′
thuộc SBcap S cap B
𝑆𝐵
).
Xét mặt phẳng (SQM′)open paren cap S cap Q cap M prime close paren
(𝑆𝑄𝑀′)
.
Cách 3 (Phổ biến nhất - Dùng mặt phẳng chứa NGcap N cap G
𝑁𝐺
và giao tuyến với (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
):Kẻ QK//SAcap Q cap K / / cap S cap A
𝑄𝐾//𝑆𝐴
( K∈ABcap K is an element of cap A cap B
𝐾∈𝐴𝐵
). Ta có mặt phẳng (SQK)open paren cap S cap Q cap K close paren
(𝑆𝑄𝐾)
cắt (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
theo giao tuyến SKcap S cap K
𝑆𝐾
.
Vì NG//(SAB)cap N cap G / / open paren cap S cap A cap B close paren
𝑁𝐺//(𝑆𝐴𝐵)
, ta có NG//SKcap N cap G / / cap S cap K
𝑁𝐺//𝑆𝐾
.
Trong △SKCtriangle cap S cap K cap C
△𝑆𝐾𝐶
, có Qcap Q
𝑄
trung điểm DCcap D cap C
𝐷𝐶
, QG//SKcap Q cap G / / cap S cap K
𝑄𝐺//𝑆𝐾
(suy ra từ NG//SKcap N cap G / / cap S cap K
𝑁𝐺//𝑆𝐾
và Gcap G
𝐺
trên SQcap S cap Q
𝑆𝑄
).
Áp dụng định lý Menelaus cho △ADCtriangle cap A cap D cap C
△𝐴𝐷𝐶
và đường thẳng qua N,G,Qcap N comma cap G comma cap Q
𝑁,𝐺,𝑄
(cần một điểm khác).
Cách 4 (Dùng mặt phẳng chứa NGcap N cap G
𝑁𝐺
và giao tuyến với (SBC)open paren cap S cap B cap C close paren
(𝑆𝐵𝐶)
hoặc (SAD)open paren cap S cap A cap D close paren
(𝑆𝐴𝐷)
):Kẻ QM′′//SBcap Q cap M double prime / / cap S cap B
𝑄𝑀′′//𝑆𝐵
( M′′∈SCcap M double prime is an element of cap S cap C
𝑀′′∈𝑆𝐶
).
Xét mặt phẳng (SQM′′)open paren cap S cap Q cap M double prime close paren
(𝑆𝑄𝑀′′)
.
Cách 5 (Quan trọng nhất): Xét mặt phẳng (SAC)open paren cap S cap A cap C close paren
(𝑆𝐴𝐶)
và đường thẳng NGcap N cap G
𝑁𝐺
.Kẻ QI//SAcap Q cap I / / cap S cap A
𝑄𝐼//𝑆𝐴
( I∈ACcap I is an element of cap A cap C
𝐼∈𝐴𝐶
) (Không có lợi).
Hãy xét mặt phẳng (SCD)open paren cap S cap C cap D close paren
(𝑆𝐶𝐷)
và đường thẳng NGcap N cap G
𝑁𝐺
.
Kẻ GK//ACcap G cap K / / cap A cap C
𝐺𝐾//𝐴𝐶
( K∈SAcap K is an element of cap S cap A
𝐾∈𝑆𝐴
).
Xét mặt phẳng (SAD)open paren cap S cap A cap D close paren
(𝑆𝐴𝐷)
: Kẻ QH//SAcap Q cap H / / cap S cap A
𝑄𝐻//𝑆𝐴
( H∈ADcap H is an element of cap A cap D
𝐻∈𝐴𝐷
).
Xét mặt phẳng (SBC)open paren cap S cap B cap C close paren
(𝑆𝐵𝐶)
: Kẻ QI//SBcap Q cap I / / cap S cap B
𝑄𝐼//𝑆𝐵
( I∈SCcap I is an element of cap S cap C
𝐼∈𝑆𝐶
).
Quay lại đường thẳng NGcap N cap G
𝑁𝐺
và mặt phẳng (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
:Vì NG//(SAB)cap N cap G / / open paren cap S cap A cap B close paren
𝑁𝐺//(𝑆𝐴𝐵)
, ta có NG//(mp(SAB))cap N cap G / / open paren m p open paren cap S cap A cap B close paren close paren
𝑁𝐺//(𝑚𝑝(𝑆𝐴𝐵))
và Gcap G
𝐺
thuộc SQcap S cap Q
𝑆𝑄
.
Gọi Mcap M
𝑀
là giao điểm của SQcap S cap Q
𝑆𝑄
với mặt phẳng (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
. Mcap M
𝑀
chính là Scap S
𝑆
. (Không đúng).
Gọi Mcap M
𝑀
là giao điểm của SQcap S cap Q
𝑆𝑄
với mặt phẳng (SAB)open paren cap S cap A cap B close paren
(𝑆𝐴𝐵)
. Mcap M
𝑀
chính là Scap S
𝑆
(Nếu Qcap Q
𝑄
không thuộc ABcap A cap B
𝐴𝐵
).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6220
Đã trả lời bởi chuyên gia
6220 -
 Đã trả lời bởi chuyên gia
5618
Đã trả lời bởi chuyên gia
5618 -
 Đã trả lời bởi chuyên gia
5582
Đã trả lời bởi chuyên gia
5582 -
 Đã trả lời bởi chuyên gia
5563
Đã trả lời bởi chuyên gia
5563 -
 Đã trả lời bởi chuyên gia
5267
Đã trả lời bởi chuyên gia
5267 -
 Đã trả lời bởi chuyên gia
4820
Đã trả lời bởi chuyên gia
4820 -
 Đã trả lời bởi chuyên gia
4328
Đã trả lời bởi chuyên gia
4328 -
 Đã trả lời bởi chuyên gia
3732
Đã trả lời bởi chuyên gia
3732