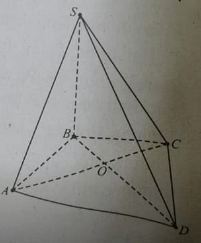
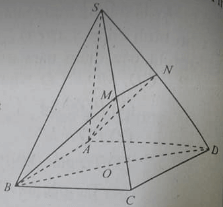
cho hình chóp S.ABCD, đáy ABCD là hình bình hành có 0 là giao điểm của hai đường chéo cho E là trung điểm của SC.
câu a. chứng minh đường thẳng OE song song với mặt phẳng SAB
câu b. tìm giao tuyến của hai mặt phẳng OED và SAD
Quảng cáo
1 câu trả lời 43
Cho hình chóp S.ABCD
ABCD là hình bình hành
O là giao điểm hai đường chéo AC và BD
E là trung điểm của SC
Câu a. Chứng minh OE song song với mặt phẳng (SAB)
Bước 1: Xét các điểm đặc biệt
Trong hình bình hành ABCD:
O là giao điểm hai đường chéo ⇒ O là trung điểm của AC
E là trung điểm của SC (theo giả thiết)
Xét tam giác SAC:
O là trung điểm của AC
E là trung điểm của SC
Bước 2: Áp dụng tính chất đường trung bình
Trong tam giác SAC, đoạn thẳng OE là đường trung bình
⇒ OE song song với SA
Bước 3: Kết luận song song với mặt phẳng
SA là đường thẳng nằm trong mặt phẳng (SAB)
OE song song với SA
Suy ra:
OE song song với mặt phẳng (SAB)
Kết luận câu a: OE ∥ (SAB)
Câu b. Tìm giao tuyến của hai mặt phẳng (OED) và (SAD)
Bước 1: Xác định các điểm chung
Điểm D thuộc:
Mặt phẳng (OED)
Mặt phẳng (SAD)
⇒ D là điểm chung
Điểm E thuộc mặt phẳng (OED)
Điểm E nằm trên SC
S, A, D xác định mặt phẳng (SAD)
Ta cần tìm một điểm chung thứ hai
Bước 2: Xét quan hệ song song
Ở câu a đã có: OE ∥ SA
OE ⊂ (OED)
SA ⊂ (SAD)
Hai mặt phẳng (OED) và (SAD) chứa hai đường thẳng song song
Bước 3: Xác định giao tuyến
Giao tuyến của hai mặt phẳng là đường thẳng đi qua D và song song với SA (hay OE)
Gọi giao tuyến là d
Kết luận cuối cùng
Câu a: OE song song với mặt phẳng (SAB)
Câu b: Giao tuyến của hai mặt phẳng (OED) và (SAD) là đường thẳng đi qua D và song song với OE (hay song song với SA)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6206
Đã trả lời bởi chuyên gia
6206 -
 Đã trả lời bởi chuyên gia
5600
Đã trả lời bởi chuyên gia
5600 -
 Đã trả lời bởi chuyên gia
5566
Đã trả lời bởi chuyên gia
5566 -
 Đã trả lời bởi chuyên gia
5544
Đã trả lời bởi chuyên gia
5544 -
 Đã trả lời bởi chuyên gia
5257
Đã trả lời bởi chuyên gia
5257 -
 Đã trả lời bởi chuyên gia
4804
Đã trả lời bởi chuyên gia
4804 -
 Đã trả lời bởi chuyên gia
4310
Đã trả lời bởi chuyên gia
4310 -
 Đã trả lời bởi chuyên gia
3717
Đã trả lời bởi chuyên gia
3717