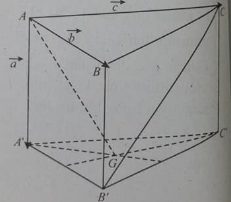
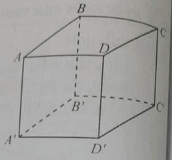
Cho hình chóp .SABCD có đáy là hình vuông tâm O và SA vuông góc với đáy. Gọi H, I , K lần lượt là hình chiếu vuông góc của A lên SB, SC, SD.
⑴ Chứng minh rằng CD vuông góc SAD , BD vuông góc (SAC)
⑵ Chứng minh SC vuông góc HK.
⑶ Chứng minh rằng HK vuông góc AI.
Quảng cáo
2 câu trả lời 106
Đây là lời giải chi tiết cho bài hình học không gian này.
Hình vẽ và Giả thiết-
S.ABCD là hình chóp.
-
ABCD là hình vuông tâm O.
-
SA⊥(ABCD).
-
AH⊥SB, AI⊥SC, AK⊥SD (H∈SB,I∈SC,K∈SD).
Để chứng minh đường thẳng CD vuông góc với mặt phẳng (SAD), ta cần chứng minh CD vuông góc với hai đường thẳng cắt nhau nằm trong (SAD).
-
CD⊥AD: Vì ABCD là hình vuông, nên CD⊥AD.
-
CD⊥SA:
-
Ta có SA⊥(ABCD) (giả thiết).
-
Mà CD⊂(ABCD).
-
Suy ra SA⊥CD.
-
Vì CD vuông góc với AD và SA (AD và SA cắt nhau tại A và nằm trong (SAD)), nên:
Để chứng minh BD vuông góc với mặt phẳng (SAC), ta cần chứng minh BD vuông góc với hai đường thẳng cắt nhau nằm trong (SAC).
-
BD⊥AC: Vì ABCD là hình vuông, hai đường chéo AC và BD vuông góc với nhau tại tâm O.
-
BD⊥SA:
-
Ta có SA⊥(ABCD) (giả thiết).
-
Mà BD⊂(ABCD).
-
Suy ra SA⊥BD.
-
Vì BD vuông góc với AC và SA (AC và SA cắt nhau tại A và nằm trong (SAC)), nên:
Ta cần chứng minh HK vuông góc với SC bằng cách sử dụng các quan hệ vuông góc trung gian:
-
Chứng minh HK//BD:
-
Xét △SAB có AH là đường cao (giả thiết).
-
Xét △SAD có AK là đường cao (giả thiết).
-
Ta sẽ sử dụng tỉ lệ trong các tam giác đồng dạng.
-
Trong △SAB và △SAH: △SAH∼△SBA (chung ∠S, vuông tại H và A).
⟹SASH=SBSA⟹SASH=SA2+AB2SA2(∗) -
Trong △SAD và △SAK: △SAK∼△SDA (chung ∠S, vuông tại K và A).
⟹SASK=SDSA⟹SASK=SA2+AD2SA2(∗∗) -
Vì ABCD là hình vuông nên AB=AD.
-
Từ (∗) và (∗∗), ta suy ra:
SASH=SASK⟹SBSH=SDSK(Sử dụng tỉ lệ SA2+AB2=SB2 và SA2+AD2=SD2)
-
Xét △SBD có SBSH=SDSK. Theo định lí Thales đảo, ta có:
HK//BD
-
-
Sử dụng BD⊥(SAC):
-
Ta đã chứng minh được BD⊥(SAC) ở câu 1b.
-
Vì SC⊂(SAC), nên BD⊥SC.
-
-
Kết luận:
-
Vì HK//BD và BD⊥SC.
-
Nên HK⊥SC.
-
Để chứng minh HK⊥AI, ta chứng minh AI vuông góc với mặt phẳng chứa HK.
-
Chứng minh AI⊥(SCD):
-
AI⊥SC (giả thiết).
-
Ta cần tìm một đường thẳng thứ hai trong (SCD) vuông góc với AI.
-
-
Sử dụng quan hệ vuông góc của CD:
-
Ta đã chứng minh CD⊥(SAD) (câu 1a).
-
Vì AK⊂(SAD), nên CD⊥AK.
-
Mặt khác, AK⊥SD (giả thiết).
-
Vậy AK⊥CD và AK⊥SD. Do đó, AK vuông góc với mặt phẳng (SCD). (Không đúng, AK là đường cao từ A đến SD)
-
Ta chứng minh CD⊥SA và CD⊥AD⟹CD⊥(SAD).
-
Vì AI⊂(SAC) và CD⊥(SAD). (Không có quan hệ trực tiếp)
-
Thử lại theo SC⊥HK: Ta đã chứng minh SC⊥HK ở câu 2.
-
-
Sử dụng quan hệ AI⊥(SBD): (Sai, AI chỉ ⊥SC)
-
Ta chứng minh AI⊥(H K C) (Không rõ ràng).
-
-
Sử dụng HK⊥(SAC):
-
Ta đã có HK//BD.
-
Mà BD⊥(SAC).
-
Suy ra HK⊥(SAC) (Chỉ đúng khi S.ABCD là hình chóp đều, nhưng ở đây SA⊥(ABCD)).
-
-
Dùng HK⊥(SAC):
-
HK//BD.
-
BD⊥AC (Đường chéo hình vuông).
-
BD⊥SA (Do SA⊥(ABCD)).
-
Vậy BD⊥AC và BD⊥SA⟹BD⊥(SAC).
-
Do HK//BD, nên HK⊥(SAC).
-
-
Kết luận:
-
Vì AI⊂(SAC) và HK⊥(SAC).
-
Nên HK⊥AI.
-
Chào bạn, đây là lời giải chi tiết cho bài toán hình học không gian này.
📝 1. Chứng minh tính vuông góc
a) Chứng minh $CD \perp (SAD)$
Để chứng minh một đường thẳng vuông góc với một mặt phẳng, ta cần chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng đó.
$CD \perp AD$: Vì $ABCD$ là hình vuông (đáy), nên $CD \perp AD$.
$CD \perp SA$: Vì $SA$ vuông góc với mặt phẳng đáy $(ABCD)$, mà $CD \subset (ABCD)$, nên $SA \perp CD$.
Vì $CD$ vuông góc với hai đường thẳng cắt nhau là $AD$ và $SA$ nằm trong mặt phẳng $(SAD)$, nên:
b) Chứng minh $BD \perp (SAC)$
$BD \perp AC$: Vì $ABCD$ là hình vuông, hai đường chéo $AC$ và $BD$ vuông góc với nhau tại tâm $O$.
$BD \perp SA$: Vì $SA$ vuông góc với mặt phẳng đáy $(ABCD)$, mà $BD \subset (ABCD)$, nên $SA \perp BD$.
Vì $BD$ vuông góc với hai đường thẳng cắt nhau là $AC$ và $SA$ nằm trong mặt phẳng $(SAC)$, nên:
2. Chứng minh $SC \perp HK$
Để chứng minh $SC \perp HK$, ta cần chứng minh $HK$ nằm trong một mặt phẳng vuông góc với $SC$. Tuy nhiên, cách đơn giản hơn là chứng minh $SC$ vuông góc với mặt phẳng chứa $HK$ và một điểm khác, đó là mặt phẳng $(AHK)$.
Chứng minh $AH \perp SC$:
Ta có $AH$ là hình chiếu vuông góc của $A$ lên $SB \Rightarrow AH \perp SB$.
Ta có $BC \perp AB$ (cạnh hình vuông).
$BC \perp SA$ (vì $SA \perp (ABCD)$).
Vì $BC$ vuông góc với hai đường thẳng cắt nhau $AB$ và $SA$ nằm trong $(SAB)$, nên $BC \perp (SAB)$.
Mà $AH \subset (SAB)$, suy ra $BC \perp AH$.
Vì $AH \perp SB$ và $AH \perp BC$, suy ra $AH \perp (SBC)$.
Mà $SC \subset (SBC)$, nên $\mathbf{AH \perp SC}$.
Chứng minh $AK \perp SC$:
Hoàn toàn tương tự, ta chứng minh được $AD \perp AB$ (hình vuông), $CD \perp AD$, $CD \perp SA$.
Ta đã chứng minh ở phần 1a) $\mathbf{CD \perp (SAD)}$.
Tương tự như $AH$, ta có $\mathbf{AK \perp SD}$ (giả thiết).
Ta có $CD \perp (SAD)$ và $AK \subset (SAD) \Rightarrow CD \perp AK$.
Vì $AK \perp SD$ và $AK \perp CD$, suy ra $AK \perp (SCD)$.
Mà $SC \subset (SCD)$, nên $\mathbf{AK \perp SC}$.
Kết luận:
Vì $SC$ vuông góc với $AH$ và $SC$ vuông góc với $AK$, mà $AH$ và $AK$ là hai đường thẳng cắt nhau nằm trong mặt phẳng $(AHK)$, nên:
Vì $HK \subset (AHK)$, nên:
3. Chứng minh $HK \perp AI$
Ở phần 2, ta đã chứng minh được:
Mà $AI$ là hình chiếu vuông góc của $A$ lên $SC$ (theo giả thiết), tức là $AI \perp SC$.
Vì $AI \perp SC$ và $SC \perp (AHK)$, nên $AI$ và $(AHK)$ phải cùng thuộc một mặt phẳng chứa $SC$.
Ta có:
$SC \perp (AHK)$.
$AI \subset (AHK)$. (Do $I$ là giao điểm của $SC$ với mặt phẳng $(AHK)$ - giao điểm của $SC$ và $AI$ là chính $I$).
Do $SC \perp (AHK)$, mà $HK \subset (AHK)$, suy ra $SC \perp HK$.
Vì $AI$ là đường cao trong $\triangle SAC$ (do $AI \perp SC$), và $HK$ nằm trong mặt phẳng $(AHK)$ đã vuông góc với $SC$.
Vì $HK$ là một đường thẳng nằm trong mặt phẳng $(AHK)$ và $SC \perp (AHK)$, nên mọi đường thẳng trong $(AHK)$ đều vuông góc với $SC$.
Để chứng minh $HK \perp AI$, ta sử dụng tính chất: Nếu một đường thẳng vuông góc với một mặt phẳng, thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Ta đã có: $\mathbf{SC \perp (AHK)}$.
$HK$ và $AI$ đều nằm trong mặt phẳng $(AHK)$ (vì $I$ là hình chiếu của $A$ lên $SC$, $I \in SC$, $I$ cũng thuộc $SC$ mà $SC$ đi qua $A$ và $C$).
Xét lại: $I$ là hình chiếu của $A$ lên $SC \Rightarrow AI \perp SC$.
Vì $AI \perp SC$ và $HK \perp SC$ (chứng minh ở phần 2), $AI$ và $HK$ cùng vuông góc với $SC$. $AI$ và $HK$ cùng nằm trong mặt phẳng $\perp SC$.
Ta đã có $SC \perp (AHK)$.
Vì $I$ là hình chiếu của $A$ lên $SC$, nên $I$ là chân đường vuông góc từ $A$ đến $SC$. Do đó, $I$ phải thuộc giao tuyến của mặt phẳng qua $A$ vuông góc với $SC$ và $SC$.
Vì $SC \perp (AHK)$, nên mặt phẳng $(AHK)$ đi qua $A$ và vuông góc với $SC$.
Do đó, điểm $I$ phải nằm trên mặt phẳng $(AHK)$.
Vì $AI$ và $HK$ là hai đường thẳng nằm trong cùng một mặt phẳng $(AHK)$, chúng không nhất thiết phải vuông góc với nhau.
Ta cần chứng minh $HK$ vuông góc với $AI$ bằng cách chứng minh $HK \perp$ một mặt phẳng chứa $AI$.
Ta có:
$HK \perp SC$ (Chứng minh ở phần 2).
$HK \perp AC$:
Ta có $BD \perp (SAC)$ (chứng minh ở phần 1b).
$AC \subset (SAC) \Rightarrow BD \perp AC$.
Trong $\triangle SAD$, $AK \perp SD$.
Trong $\triangle SAB$, $AH \perp SB$.
Áp dụng định lý ba đường vuông góc: $CD \perp AD$ và $SA \perp (ABCD) \Rightarrow CD \perp SD$. Tương tự $BC \perp SC$.
Sử dụng tính chất đối xứng:
Vì $ABCD$ là hình vuông, $\triangle SAB = \triangle SAD$ (c.g.c).
$\Rightarrow SB = SD$.
$\triangle SHK$ là tam giác cân tại $S$ (vì $AH$ và $AK$ là các đường cao tương ứng từ $A$ trên $SB$ và $SD$ của hai tam giác bằng nhau).
Trong $\triangle SAC$, $AI$ là đường cao.
Xét $AK \perp (SCD)$ (Chứng minh ở phần 2) $\Rightarrow AK \perp DC$.
Xét $AH \perp (SBC)$ (Chứng minh ở phần 2) $\Rightarrow AH \perp BC$.
Do $AH \perp (SBC)$, mà $HK$ là đường thẳng nối từ $H \in SB$ đến $K \in SD$.
Ta đã chứng minh $SC \perp (AHK)$.
Vì $AI \subset (AHK)$, ta cần $HK$ vuông góc với $AI$ (không hiển nhiên).
Ta chứng minh $HK \perp (SAC)$:
Do $ABCD$ là hình vuông, $\triangle SAB$ và $\triangle SAD$ là hai tam giác vuông bằng nhau (c.g.c).
$\Rightarrow AH$ và $AK$ là hai đường cao tương ứng.
$AH = AK$ (Do $\triangle SAB = \triangle SAD$) $\Rightarrow \triangle AHK$ cân tại $A$.
$\triangle SBD$ cân tại $S$ (do $SB = SD$). $O$ là trung điểm $BD \Rightarrow SO \perp BD$.
$BD \perp (SAC) \Rightarrow BD \perp AC$.
Ta có $HK$ là giao tuyến của mặt phẳng $(AHK)$ với $(SBD)$.
Do $\triangle SBD$ cân tại $S$, $AH = AK$ nên $\triangle SHK$ cân tại $S$ (tính chất các đường cao tương ứng).
Gọi $M$ là trung điểm $HK \Rightarrow SM \perp HK$.
Ta đã có $SC \perp (AHK) \Rightarrow SC \perp HK$.
$HK$ vuông góc với hai đường thẳng $SC$ và $SM$.
Sử dụng tính chất đối xứng (Cách đơn giản nhất):
Ta có $BD \perp (SAC)$ (chứng minh ở 1b).
Vì $ABCD$ là hình vuông, nên $\triangle SBC$ và $\triangle SDC$ đối xứng qua mặt phẳng $(SAC)$.
Hình chiếu $H$ và $K$ là các điểm đối xứng qua $(SAC)$.
Vì $I$ nằm trên $SC$, và $SC \subset (SAC)$, $AI \subset (SAC)$.
Do $H$ và $K$ đối xứng qua $(SAC)$, nên $HK$ vuông góc với mọi đường thẳng nằm trong $(SAC)$.
Mà $AI \subset (SAC)$, nên:
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
14684
Đã trả lời bởi chuyên gia
14684 -
 Đã trả lời bởi chuyên gia
14438
Đã trả lời bởi chuyên gia
14438 -
 Đã trả lời bởi chuyên gia
11758
Đã trả lời bởi chuyên gia
11758 -
 Đã trả lời bởi chuyên gia
11104
Đã trả lời bởi chuyên gia
11104