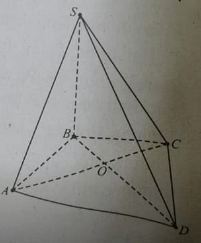
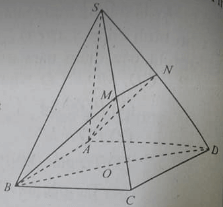
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD
a) xác định giao tuyến của 2 mặt phẳng ( SAC)và (SBD)
b) gọi M,N lần lượt là trung điểm của SD,SC .chứng minh MN song song với AB
Quảng cáo
1 câu trả lời 118
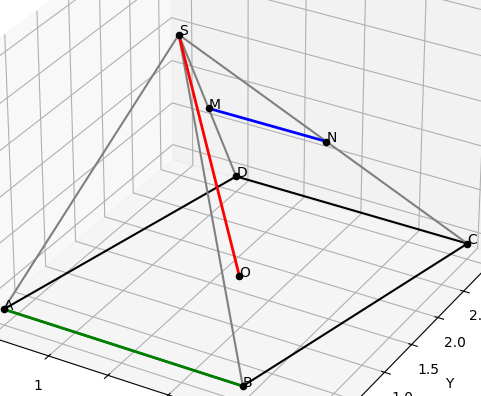
a) Xác định giao tuyến của hai mặt phẳng (SAC) và (SBD)
- Hai mặt phẳng (SAC) và (SBD):
- Cùng đi qua đỉnh chung S ⇒ giao tuyến chắc chắn đi qua S.
- Xét phần còn lại:
+ Mặt phẳng (SAC)) chứa đường chéo AC của đáy.
+ Mặt phẳng (SBD) chứa đường chéo BD của đáy.
+ Hai đường chéo AC và BD của hình bình hành cắt nhau tại trung điểm O.
Do đó: O = AC ∩ BD nằm trong cả hai mặt phẳng.
- Hai mặt phẳng đều chứa S và O.
→ Giao tuyến của hai mặt phẳng là đường thẳng SO.(SAC) ∩ (SBD) = SO
b) Gọi M, N lần lượt là trung điểm của SD và SC. Chứng minh MN // AB
Ta có:
M là trung điểm của SD ⇒ SM = MD
N là trung điểm của SC ⇒ SN = NC
- Xét tam giác SDC:
M là trung điểm của SD
N là trung điểm của SC
Trong tam giác: Đường nối hai trung điểm của hai cạnh thì song song với cạnh còn lại.
⇒ MN // DC .
- Mà đáy ABCD là hình bình hành nên: AB // DC
Vậy: MN // DC // AB
=> MN // AB (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6214
Đã trả lời bởi chuyên gia
6214 -
 Đã trả lời bởi chuyên gia
5610
Đã trả lời bởi chuyên gia
5610 -
 Đã trả lời bởi chuyên gia
5578
Đã trả lời bởi chuyên gia
5578 -
 Đã trả lời bởi chuyên gia
5560
Đã trả lời bởi chuyên gia
5560 -
 Đã trả lời bởi chuyên gia
5264
Đã trả lời bởi chuyên gia
5264 -
 Đã trả lời bởi chuyên gia
4814
Đã trả lời bởi chuyên gia
4814 -
 Đã trả lời bởi chuyên gia
4320
Đã trả lời bởi chuyên gia
4320 -
 Đã trả lời bởi chuyên gia
3726
Đã trả lời bởi chuyên gia
3726