Cho đường tròn tâm O bán kính OA = 3 cm. Kẻ đường thẳng d là tiếp tuyến của đường tròn (O) tại A. Trên đường thẳng d lấy điểm M sao cho AM = 4 cm.
a) Tính độ dài đoạn thẳng OM
b) Kẻ dây AC ⟂ OM tại H. Chứng minh MC là tiếp tuyến của đường tròn (O)
c) Kẻ đường kính AB. Gọi N là trung điểm của HM. Đường thẳng AN cắt đường tròn (O) tại điểm K (K khác A). Chứng minh 3 điểm B, H, K thẳng hàng.
Quảng cáo
4 câu trả lời 1319
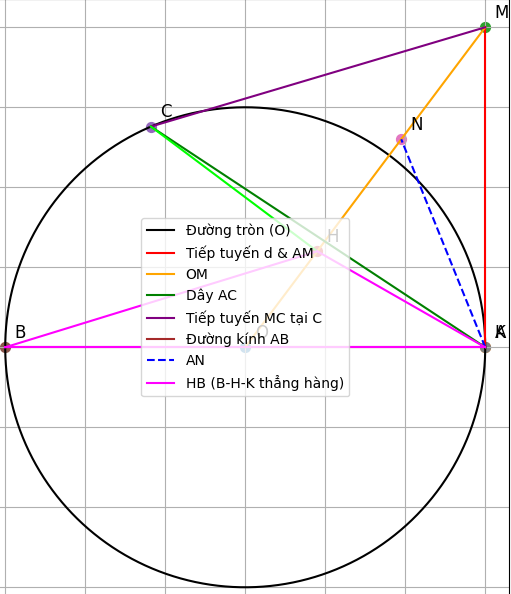
a) Tính độ dài đoạn OM
Vì d là tiếp tuyến của đường tròn (O) tại A nên: OA ⊥ d ⇒ △OAM vuông tại A.
Do đó: OM2 = OA2 + AM2 = 32 + 42 = 9 + 16 = 25.
=> OM = 5 cm.
b) Kẻ dây AC vuông góc với OM tại H. Chứng minh rằng MC là tiếp tuyến của (O).
Ta có: AC ⊥ OM tại H.
Mà OM đi qua tâm O nên: OH ⊥ AC.
=> H là chân đường vuông góc từ tâm O xuống dây AC.
Tính chất đường vuông góc từ tâm đến dây cho biết: H là trung điểm của AC.
Khi đó trong tam giác OMC có :
H là trung điểm của AC,
OH ⊥ AC, nên OC cũng vuông góc với MC (vì hai tam giác đối xứng nhau qua OH).
=> MC ⊥ OC.
Do bán kính OC vuông góc với đường thẳng MC
=> MC là tiếp tuyến của đường tròn (O) tại C.
c) Kẻ đường kính AB. Gọi N là trung điểm của HM. Đường thẳng AN cắt đường tròn tại K (≠ A). Chứng minh 3 điểm B, H, K thẳng hàng.
Vì AB là đường kính nên: = 90∘.(1)
Do AC ⊥ OM tại H, nên: H ∈ AC và H là điểm chân đường cao của tam giác ABC.(2)
Xét đường thẳng AN:
N là trung điểm của HM,
K là giao điểm thứ hai của AN với đường tròn (O).
Ta dùng tính chất quan trọng: Định lý Simson
Với một điểm K nằm trên đường tròn ngoại tiếp tam giác ABC, chân các đường vuông góc từ K đến ba cạnh của tam giác nằm thẳng hàng (gọi là đường Simson).
- Áp dụng cho tam giác ABC:
Do H là chân đường vuông góc từ C xuống AB,
Đường AN cắt lại đường tròn tại K nên K đối xứng với M qua H,
Suy ra H là chân đường vuông góc từ K xuống BC.
Do đó ba chân đường vuông góc ứng với điểm K nằm thẳng hàng; đặc biệt:
H, B, K thẳng hàng.
Vậy: B, H, K thẳng hàng.
𝑂𝑀
là 5cm5 cm
5cm
.
b) MCcap M cap C
𝑀𝐶
là tiếp tuyến của đường tròn (O)open paren cap O close paren
(𝑂)
.
c) Ba điểm B,H,Kcap B comma cap H comma cap K
𝐵,𝐻,𝐾
thẳng hàng.
Vì d là tiếp tuyến của đường tròn (O) tại A nên: OA ⊥ d ⇒ △OAM vuông tại A.
Do đó: OM2 = OA2 + AM2 = 32 + 42 = 9 + 16 = 25.
=> OM = 5 cm.
b) Kẻ dây AC vuông góc với OM tại H. Chứng minh rằng MC là tiếp tuyến của (O).
Ta có: AC ⊥ OM tại H.
Mà OM đi qua tâm O nên: OH ⊥ AC.
=> H là chân đường vuông góc từ tâm O xuống dây AC.
Tính chất đường vuông góc từ tâm đến dây cho biết: H là trung điểm của AC.
Khi đó trong tam giác OMC có :
H là trung điểm của AC,
OH ⊥ AC, nên OC cũng vuông góc với MC (vì hai tam giác đối xứng nhau qua OH).
=> MC ⊥ OC.
Do bán kính OC vuông góc với đường thẳng MC
=> MC là tiếp tuyến của đường tròn (O) tại C.
c) Kẻ đường kính AB. Gọi N là trung điểm của HM. Đường thẳng AN cắt đường tròn tại K (≠ A). Chứng minh 3 điểm B, H, K thẳng hàng.
Vì AB là đường kính nên: ˆACB = 90∘.(1)
Do AC ⊥ OM tại H, nên: H ∈ AC và H là điểm chân đường cao của tam giác ABC.(2)
Xét đường thẳng AN:
N là trung điểm của HM,
K là giao điểm thứ hai của AN với đường tròn (O).
Ta dùng tính chất quan trọng: Định lý Simson
Với một điểm K nằm trên đường tròn ngoại tiếp tam giác ABC, chân các đường vuông góc từ K đến ba cạnh của tam giác nằm thẳng hàng (gọi là đường Simson).
- Áp dụng cho tam giác ABC:
Do H là chân đường vuông góc từ C xuống AB,
Đường AN cắt lại đường tròn tại K nên K đối xứng với M qua H,
Suy ra H là chân đường vuông góc từ K xuống BC.
Do đó ba chân đường vuông góc ứng với điểm K nằm thẳng hàng; đặc biệt:
H, B, K thẳng hàng.
Vậy: B, H, K thẳng hàng.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8426
Đã trả lời bởi chuyên gia
8426 -
 Đã trả lời bởi chuyên gia
7105
Đã trả lời bởi chuyên gia
7105 -
 Đã trả lời bởi chuyên gia
6856
Đã trả lời bởi chuyên gia
6856 -
 Đã trả lời bởi chuyên gia
6781
Đã trả lời bởi chuyên gia
6781 -
 Đã trả lời bởi chuyên gia
5472
Đã trả lời bởi chuyên gia
5472 -
 Đã trả lời bởi chuyên gia
5350
Đã trả lời bởi chuyên gia
5350 -
 Đã trả lời bởi chuyên gia
5082
Đã trả lời bởi chuyên gia
5082