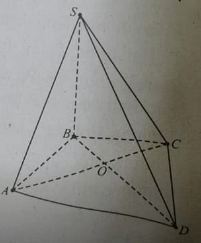
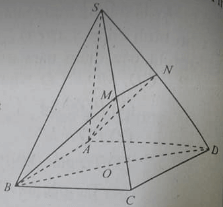
Bài 9. Cho hình chóp S.ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh SB,

· 09:54 22/08/2025

Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

Bài 9. Cho hình chóp S.ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh SB, SA, AC.

a) Trong các đoạn thẳng SA, SB, SC, AB, BC, CA, MN đoạn nào nhìn thấy (vẽ nét liền), đoạn nào bị che khuất (vẽ nét đứt)?

b) Đường thẳng MN có cắt đường thẳng AB hay không? Vì sao?

c) Đường thẳng MB có cắt đường thẳng SC hay không? Vì sao?

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

3 câu trả lời 837

Gia Hân

3 tháng trước

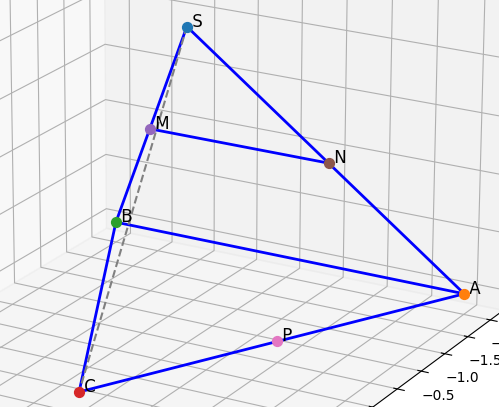
Hỏi đáp VietJack

a) Đoạn nào nhìn thấy (nét liền), đoạn nào bị khuất (nét đứt)?
Nhìn thấy (vẽ nét liền):
=> SA, SB, AB, BC, AC, MN
Bị khuất (vẽ nét đứt):
=> SC, NP (nếu cần vẽ để rõ hơn)

b) Đường thẳng MN có cắt đường thẳng AB hay không? Vì sao?
MN nối trung điểm của SB và SA
AB nằm dưới đáy (mặt phẳng ABC), MN nằm trên mặt bên của hình chóp
→ Hai đường không đồng phẳng → Không thể cắt nhau
=> Trả lời: Không cắt, vì không đồng phẳng

c) Đường thẳng MB có cắt SC không? Vì sao?
MB nối từ trung điểm SB đến điểm B
SC là cạnh bên của chóp
→ Hai đường này cũng không đồng phẳng, không nằm trong cùng mặt phẳng nào xác định

=> Trả lời: Không cắt, vì không đồng phẳng

0 bình luận

Đăng nhập để hỏi chi tiết

n.duck.duy

3 tháng trước

Dưới đây là lời giải chi tiết cho Bài 9 về hình học không gian – hình chóp S.ABC với các trung điểm M, N, P của SB, SA, AC tương ứng:

🔹 TÓM TẮT ĐỀ BÀI

Cho hình chóp $S . A B C$ S.ABC.
Gọi:

$M$ M: trung điểm của cạnh $S B$ SB,
$N$ N: trung điểm của cạnh $S A$ SA,
$P$ P: trung điểm của cạnh $A C$ AC.

Yêu cầu:

a) Cho biết các đoạn: SA, SB, SC, AB, BC, CA, MN – đoạn nào nhìn thấy (vẽ nét liền), đoạn nào bị khuất (vẽ nét đứt)? b) Đường thẳng

M N

MN có cắt đường thẳng

A B

AB không? Vì sao? c) Đường thẳng

M B

MB có cắt đường thẳng

M

0SC không? Vì sao? ✅ Giải chi tiết 🔸 a) Nhìn thấy hay bị khuất

Để trả lời câu này, ta cần xác định vị trí các điểm trong không gian và hình dạng hình chóp S.ABC, từ đó suy ra tầm nhìn.

Giả sử hình chóp S.ABC được vẽ theo quy ước phổ biến:
Mặt phẳng đáy $M$ 1ABC nằm trong mặt phẳng ngang (phía dưới), đỉnh $M$ 2S nằm phía trên đáy.

Dựa vào quy ước phối cảnh, ta có:

Các cạnh nối đỉnh với đáy (SA, SB, SC):
→ SA và SB thường bị khuất phía sau mặt phẳng đáy nếu ta nhìn từ phía trước (tùy góc nhìn).
→ SC thường nhìn thấy rõ nhất.
Các cạnh của đáy (AB, BC, CA):
→ AB thường bị khuất phía sau nếu ta nhìn từ phía trước – vì có thể bị SA, SB che.
→ BC thường nhìn thấy
→ CA thường nhìn thấy
MN là đoạn nối 2 trung điểm của SB và SA
→ Vì SB và SA nằm phía sau, đoạn MN cũng thường bị khuất.

Tuy nhiên, nếu đề không cho hình vẽ cụ thể, ta phải dựa trên quy ước chuẩn của hình chóp vẽ trên mặt phẳng 2D, trong đó:

👉 Kết luận a)

Đoạn	Tình trạng
SA	Khuất (nét đứt)
SB	Khuất (nét đứt)
SC	Thấy (nét liền)
AB	Khuất (nét đứt)
BC	Thấy (nét liền)
CA	Thấy (nét liền)
MN	Khuất (nét đứt)

🔸 b) Đường thẳng MN có cắt AB không? Vì sao?

$M$ M là trung điểm của $S B$ SB
$N$ N là trung điểm của $S A$ SA

→ Suy ra đoạn $M N$ MN nằm trên mặt phẳng (SAB)

$A B$ AB là cạnh đáy ⇒ cũng thuộc mặt phẳng $M$ 9(SAB)

➡️ Do đó: MN và AB cùng thuộc mặt phẳng (SAB).

Tuy nhiên:

$M N$ MN nối 2 điểm nằm trên các cạnh bên, còn $A B$ AB nằm dưới đáy, không có điểm chung với $M N$ MN

→ Hai đoạn thẳng này không đồng quy, không cắt nhau.

Cách lý luận hình học:
MN nối trung điểm SB và SA → MN là đường trung bình của tam giác SAB.
AB là đáy của tam giác SAB.
→ MN song song và không cắt AB.

👉 Kết luận b):

Không, đường thẳng $M N$ MN không cắt đường thẳng $A B$ AB, vì:

Cùng nằm trên mặt phẳng (SAB),
Nhưng $S B$ 5MN∥AB (do là đường trung bình tam giác SAB).

🔸 c) Đường thẳng MB có cắt đường thẳng SC không? Vì sao?

$M$ M là trung điểm của $S B$ SB, nên $M B$ MB nằm trên mặt phẳng (SBC)
$M$ 0SC cũng nằm trong mặt phẳng (SBC)

➡️ Hai đường thẳng $M B$ MB và $M$ 0SC cùng thuộc mặt phẳng (SBC)

Xét trên mặt phẳng (SBC):

$M B$ MB là đoạn nối trung điểm của SB đến đỉnh B → nằm trong tam giác SBC
$M$ 0SC là cạnh tam giác đó

→ Hai đoạn này không đồng quy, cũng không song song, có thể cắt nhau tại một điểm trong mặt phẳng.

Tuy nhiên, cần xét rõ vị trí:

MB nối trung điểm SB và B
SC nối từ đỉnh S đến C

Chúng có thể cắt nhau tại một điểm nằm bên trong mặt phẳng (SBC)

👉 Kết luận c):

Có, đường thẳng $M B$ MB cắt đường thẳng $M$ 0SC, vì:

Cùng nằm trong mặt phẳng (SBC)
Không song song, không trùng, nên cắt nhau tại một điểm duy nhất trong mặt phẳng đó.

✅ Tóm tắt kết luận

Câu hỏi	Kết luận
a)	SA, SB, AB, MN: bị khuất (nét đứt) SC, BC, CA: nhìn thấy (nét liền)
b)	MN không cắt AB, vì MN là đường trung bình tam giác SAB ⇒ song song AB
c)	MB cắt SC, vì cùng thuộc mặt phẳng (SBC) và không song song