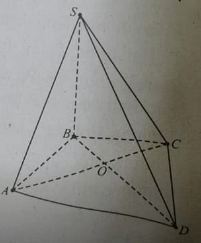
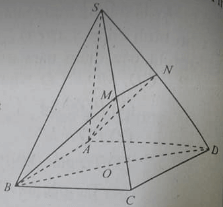
Trong mặt phẳng alpha , cho hình bình hành ABCD tâm O, S là một điểm không thuộc alpha . Gọi M,N, P lần lượt là trung điểm của BC, CD và SO. Đường thẳng MN cắt AB, AC và AD tạ M1, N1 và O1. Nối N1P cắt SA tại P1, nối M1P1 cắt SB tại M2, nối O1P1 cắt SD tại N2.
a) Xác định giao tuyến của (MNP) với (SAB).
b) Xác định giao tuyến của ( MNP) với (SAD).
c) Xác định giao tuyến của ( MNP) với (SCD).
d) Xác định giao tuyến của (MNP) với đường thẳng SB
e) Hình tạo bởi mp(ABCD) và điểm S không thuộc mp(ABCD) (hình S.ABCD) gồm mấy mặt? còn được gọi là hình gì?
f) Hình tạo bởi mp(ABC) và điểm S không thuộc mp(ABC) (hình S.ABC) gồm mấy mặt? còn được gọi là hình gì?
Quảng cáo
2 câu trả lời 2468
a) Giao tuyến của (MNP) với (SAB) là đường thẳng AB. Để giải thích điều này, ta có thể sử dụng các bước sau:
Vì M, N lần lượt là trung điểm của các cạnh SB, BC nên MN là đường trung bình của tam giác SBC, do đó MN // SC.
Mà MN ⊂ (MNP). Từ đó suy ra SC // (MNP).
Do đó, (MNP) và (SAB) đồng quy.
b) Giao tuyến của (MNP) với (SAD) là đường thẳng AD. Để giải thích điều này, ta có thể sử dụng các bước sau:
Gọi Q là trung điểm của SD, mà P là trung điểm của CD nên PQ là đường trung bình của tam giác SCD nên SC // QP.
Mà MN ⊂ (MNP). Từ đó suy ra MN // QP.
Do đó, (MNP) và (SAD) đồng quy.
c) Giao tuyến của (MNP) với (SCD) là đường thẳng CD. Để giải thích điều này, ta có thể sử dụng các bước sau:
Vì N, P lần lượt là trung điểm của các cạnh CD, SO nên NP là đường trung bình của tam giác SCD, do đó NP // SC.
Mà NP ⊂ (MNP). Từ đó suy ra SC // (MNP).
Do đó, (MNP) và (SCD) đồng quy.
d) Giao tuyến của (MNP) với đường thẳng SB là đường thẳng M2B. Để giải thích điều này, ta có thể sử dụng các bước sau:
Gọi P1 là giao điểm của đường thẳng N1P và SA.
Ta có M1P1 // SB (do M1P1 là đường trung bình của tam giác SBO).
Mà M1P1 ⊂ (MNP). Từ đó suy ra M2B // (MNP).
Do đó, (MNP) và đường thẳng SB đồng quy.
e) Hình tạo bởi mp(ABCD) và điểm S không thuộc mp(ABCD) (hình S.ABCD) gồm 2 mặt. Đó là mặt đáy ABCD và mặt bên SCD. Hình S.ABCD còn được gọi là hình chóp tứ giác.
f) Hình tạo bởi mp(ABC) và điểm S không thuộc mp(ABC) (hình S.ABC) gồm 3 mặt. Đó là mặt đáy ABC, mặt bên SBC và mặt bên SAC. Hình S.ABC còn được gọi là hình chóp tam giác.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6214
Đã trả lời bởi chuyên gia
6214 -
 Đã trả lời bởi chuyên gia
5610
Đã trả lời bởi chuyên gia
5610 -
 Đã trả lời bởi chuyên gia
5578
Đã trả lời bởi chuyên gia
5578 -
 Đã trả lời bởi chuyên gia
5560
Đã trả lời bởi chuyên gia
5560 -
 Đã trả lời bởi chuyên gia
5264
Đã trả lời bởi chuyên gia
5264 -
 Đã trả lời bởi chuyên gia
4814
Đã trả lời bởi chuyên gia
4814 -
 Đã trả lời bởi chuyên gia
4320
Đã trả lời bởi chuyên gia
4320 -
 Đã trả lời bởi chuyên gia
3726
Đã trả lời bởi chuyên gia
3726