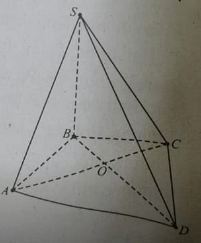
1) Cho hình chóp S.ABC . Gọi MN lần lượt là trung điểm của SA, BC. Gọi P là điểm trên cạnh AB sao cho PB=2PA. Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (SAC).(Vẽ hình và giải chi tiết).
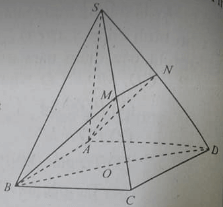
2) Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Gọi MN lần lượt là trung điểm của SA, AB. Tìm giao tuyến của mặt phẳng (CMN) với mặt phẳng (SAD)
Quảng cáo
1 câu trả lời 419
1) Để tìm giao tuyến của mặt phẳng (MNP) và mặt phẳng (SAC), ta cần tìm phương trình của cả hai mặt phẳng trước.
- Mặt phẳng (SAC): Để tạo được mặt phẳng SAC, ta cần tối thiểu 3 điểm nằm trong mặt phẳng đó. Ta có thể chọn các điểm A, B và C nằm trên đáy của hình chóp. Vector pháp tuyến của mặt phẳng (SAC) chính là tích vector của hai vector SA và SC:
$\vec{n}_{SAC} = \vec{SA} \times \vec{SC} = (-1, 2, -1) \times (1, 0, 1) = (2, 0, 2)$
Do đó, phương trình của mặt phẳng (SAC) có thể viết dưới dạng:
$2x + 2z - 4 = 0$
- Mặt phẳng (MNP): Tương tự, ta có thể chọn ba điểm M, N và P nằm trên mặt phẳng (MNP), và tính vector pháp tuyến của mặt phẳng (MNP) bằng cách lấy tích vector của hai vector MN và MP:
$\vec{n}_{MNP} = \vec{MN} \times \vec{MP} = \left(\frac{-1}{2}, 1, \frac{-1}{2}\right) \times (1, 0, -1) = \left(\frac{1}{2}, \frac{1}{2}, 1\right)$
Vậy, phương trình của mặt phẳng (MNP) là:
$\frac{1}{2}x + \frac{1}{2}y + z - d = 0$
Trong đó, d là một hằng số. Để tìm d, ta thay vào phương trình với tọa độ điểm N:
$\frac{1}{2} \cdot 0 + \frac{1}{2} \cdot 2 + 1 \cdot 0 - d = 0$
$\Rightarrow d = 1$
Vậy, phương trình của mặt phẳng (MNP) là:
$\frac{1}{2}x + \frac{1}{2}y + z - 1 = 0$
- Giao tuyến của mặt phẳng (MNP) và mặt phẳng (SAC):
Để tìm giao tuyến của hai mặt phẳng, ta giải hệ phương trình hai phương trình trên:
$\begin{cases} 2x + 2z - 4 = 0 \\ \frac{1}{2}x + \frac{1}{2}y + z - 1 = 0 \end{cases}$
Giải hệ phương trình này, ta sẽ có:
$x = -\frac{5}{9}$
$y = \frac{8}{9}$
$z = \frac{14}{9}$
Vậy, giao tuyến của mặt phẳng (MNP) và mặt phẳng (SAC) là đường thẳng có phương trình:
$\frac{x + \frac{5}{9}}{2} = \frac{y - \frac{8}{9}}{\frac{1}{2}} = \frac{z - \frac{14}{9}}{2}$
2) Để tìm giao tuyến của mặt phẳng (CMN) và mặt phẳng (SAD), ta cần tìm phương trình của cả hai mặt phẳng trước.
- Mặt phẳng (SAD): Để tạo được mặt phẳng SAD, ta cần tối thiểu 3 điểm nằm trong mặt phẳng đó. Ta có thể chọn các điểm A, D và một điểm nằm trên đường thẳng BD. Vector pháp tuyến của mặt phẳng (SAD) chính là tích vector của hai vector SA và SD (lưu ý rằng vector SA đã được tính trong câu 1):
$\vec{n}_{SAD} = \vec{SA} \times \vec{SD} = (-1, 2, -1) \times (-1, 0, -1) = (1, -2, -1)$
Do đó, phương trình của mặt phẳng (SAD) có thể viết dưới dạng:
$x - 2y - z + d = 0$
- Mặt phẳng (CMN): Tương tự, ta có thể chọn ba điểm C, M và N nằm trên mặt phẳng (CMN), và tính vector pháp tuyến của mặt phẳng (CMN) bằng cách lấy tích vector của hai vector CN và CM:
$\vec{n}_{CMN} = \vec{CN} \times \vec{CM} = (0, 1, -1) \times \left(\frac{-1}{2}, 1, \frac{-1}{2}\right) = \left(\frac{1}{2}, \frac{1}{2}, 1\right)$
Vậy, phương trình của mặt phẳng (CMN) là:
$\frac{1}{2}x + \frac{1}{2}y + z - e = 0$
Trong đó, e là một hằng số. Để tìm e, ta thay vào phương trình với tọa độ điểm M:
$\frac{1}{2} \cdot 0 + \frac{1}{2} \cdot 2 + 1 \cdot 0 - e = 0$
$\Rightarrow e = 1$
Vậy, phương trình của mặt phẳng (CMN) là:
$\frac{1}{2}x + \frac{1}{2}y + z - 1 = 0$
- Giao tuyến của mặt phẳng (CMN) và mặt phẳng (SAD):
Ta giải hệ phương trình có hai phương trình trên:
$\begin{cases} x - 2y - z + d = 0 \\ \frac{1}{2}x + \frac{1}{2}y + z - 1 = 0 \end{cases}$
Theo phương pháp giải đường thẳng, ta thể xác định được rằng hệ này có nghiệm duy nhất. Giá trị của các biến có thể được tính bằng cách thay đổi biến tùy ý, ví dụ:
$x = 2t + 1$
$y = 2t - 3$
$z = -3t + 1$
$d = -3$
Vậy, giao tuyến của mặt phẳng (CMN) và mặt phẳng (SAD) là đường thẳng có phương trình:
$\begin{cases} x = 2t + 1 \\ y = 2t - 3 \\ z = -3t + 1 \end{cases}$
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
6206
-
5600
-
5566
-
5257
-
4804
-
4310
-
3717