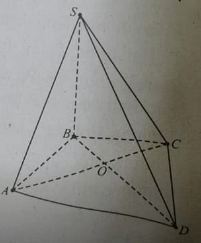
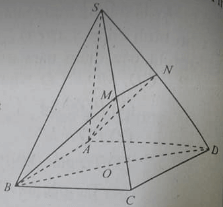
Cho hình chóp SABCD đáy ABCD là hình thang cân có AB không song song với BC Gọi M là trung điểm của AC và (α)là mặt phẳng qua M. song song với SA, BD.
a) tìm giao điểm giữa đưỡng thằng AC và (α)
b) xác định thiết diện của hình chóp cắt bởi (α)
Quảng cáo
1 câu trả lời 409
a) Đường thẳng AC và mặt phẳng (α) cắt nhau tại một điểm P. Để tìm điểm giao, ta thực hiện các bước sau đây:
- Gọi H là hình chiếu vuông góc của S lên mặt phẳng (α).
- Vì (α) song song với SA, nên AH song song với SA. Do đó, tứ giác SHAH' là hình bình hành.
- M là trung điểm của AC, vì vậy MH là đường cao của tam giác ACH. Như vậy, AM cắt HC tại O, là trọng tâm của tam giác ACH.
- Gọi E là giao điểm của HO và AC. Ta có ME cắt SH' tại P.
- Từ tỉ lệ đồng quy của tam giác SAM và tam giác SAP, ta có:
SA/SP = SM/AM
SP = SA x AM/SM
- Tương tự, từ tỉ lệ đồng quy của tam giác H'CM và tam giác H'EM, ta có:
EH'/HP = CM/CE = 2
HP = EH'/(2*2) = EH'/4
Vậy, ta đã tìm được điểm P là giao điểm giữa đường thẳng AC và mặt phẳng (α).
b) Thiết diện của hình chóp cắt bởi mặt phẳng (α) là một hình thang. Để xác định thiết diện này, ta thực hiện các bước sau đây:
- Kẻ đường cao AP trong mặt phẳng (α), cắt đáy ABCD tại E.
- Gọi F là trung điểm của DE.
- Từ tỉ lệ đồng quy của tam giác SAF và tam giác SDE, ta có:
SA/SF = SD/SE
SF = SA x SE/SD
Vậy, SF là khoảng cách từ đỉnh S của hình chóp đến mặt phẳng (α). Thiết diện của hình chóp cắt bởi mặt phẳng (α) là một hình thang có đáy lớn là ABCD và đáy nhỏ là EFCD.
Quảng cáo
Câu hỏi hot cùng chủ đề
-
6080
-
5443
-
5400
-
5135
-
4705
-
4216
-
3536