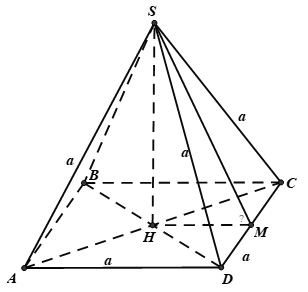
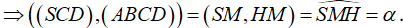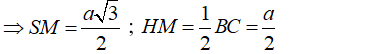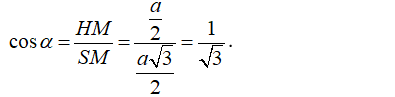Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa một mặt bên và một mặt đáy.
A.
B.
C.
D.
Quảng cáo
1 câu trả lời 487
Chọn C.
+) Giả sử gọi hình chóp tứ giác đều có tất cả các cạnh đều bằng a là S.ABCD có đường cao SH. Trong đó, H là tâm của hình vuông ABCD.
+) Ta có: (SCD) ∩ (ABCD) = CD. Gọi M là trung điểm CD.
- Tam giác SCD có SC = SD = a nên tam giác cân tại S, có SM là đường trung tuyến nên đồng thời là đường cao: SM ⊥ CD.
- Tam giác HCD cân tại H (HC = HD = AC/2 = BD/2)
có HM là đường trung tuyến nên đồng thời là đường cao: HM ⊥ CD.
+) Ta có : SC = SD = CD = a nên tam giác SCD là tam giác đều cạnh a có SM là đường trung tuyến:
- Trong tam giác vuông SHM vuông tại H có:
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
32574
Đã trả lời bởi chuyên gia
32574 -
 Đã trả lời bởi chuyên gia
27808
Đã trả lời bởi chuyên gia
27808 -
 Đã trả lời bởi chuyên gia
26789
Đã trả lời bởi chuyên gia
26789 -
 Đã trả lời bởi chuyên gia
25747
Đã trả lời bởi chuyên gia
25747 -
 Đã trả lời bởi chuyên gia
20213
Đã trả lời bởi chuyên gia
20213
Gửi báo cáo thành công!