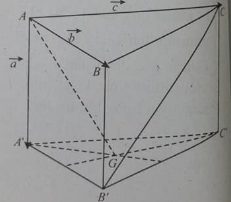
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA=OB=2OC. gọi M là trung điểm của BC, tính cosin góc của OM và AB
Quảng cáo
1 câu trả lời 1509
Đặt OA=OB=2OC=2aOA=OB=2OC=2a
⇒BC=√OB2+OC2=a√5⇒BC=OB2+OC2=a5 ⇒OM=12BC=a√52⇒OM=12BC=a52
Qua B kẻ đường thẳng song song OM cắt OC kéo dài tại D
⇒OM⇒OM là đường trung bình tam giác BCD ⇒BD=2OM=a√5⇒BD=2OM=a5
OM||BD⇒(OM;AB)=(BD;AB)=ˆABDOM||BD⇒(OM;AB)=(BD;AB)=ABD^
AB=√OA2+OB2=2a√2AB=OA2+OB2=2a2
AD=√OA2+OD2=√OA2+OC2=a√5AD=OA2+OD2=OA2+OC2=a5
⇒cosˆABD=AB2+BD2−AD22AB.BD=√105
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
14684
Đã trả lời bởi chuyên gia
14684 -
 Đã trả lời bởi chuyên gia
14438
Đã trả lời bởi chuyên gia
14438 -
 Đã trả lời bởi chuyên gia
11758
Đã trả lời bởi chuyên gia
11758 -
 Đã trả lời bởi chuyên gia
11104
Đã trả lời bởi chuyên gia
11104
Gửi báo cáo thành công!