Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng , trong đó 1abcd9
A. 0,014
B. 0,0495
C. 0,079
D. 0,055
Quảng cáo
1 câu trả lời 2159
Chọn D
Chọn số tự nhiên có 4 chữ số bất kỳ có: ![]() (cách).
(cách).
Gọi A là biến cố: “Số được chọn có dạng , trong đó 1abcd9” . (*)
Cách 1: Dùng tổ hợp
Nhận xét rằng với 2 số tự nhiên bất kỳ ta có: ![]()
Do đó nếu đặt:

Từ giả thuyết ![]() ta suy ra:
ta suy ra: ![]()
Với mỗi tập con gồm 4 phần tử đôi một khác nhau được lấy ra từ {1,2,....,12}ta đều có được duy nhất một bộ số thoả mãn (**) và do đó tương ứng ta có duy nhất một bộ số (a,b,c,d) thoả mãn (*). Số cách chọn tập con thoả tính chất trên là tổ hợp chập 4 của 12 phần tử, do đó:
![]()
Vậy 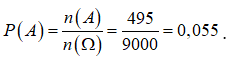
Cách 2: Dùng tổ hợp lặp
Chọn số tự nhiên có 4 chữ số bất kỳ có: ![]() (cách).
(cách).
Mỗi tập con có 4 phần tử được lấy từ tập {1,2,...,9}(trong đó mỗi phần tử có thể được chọn lặp lại nhiều lần) ta xác định được một thứ tự không giảm duy nhất và theo thứ tự đó ta có được một số tự nhiên có dạng (trong đó ![]() ). Số tập con thoả tính chất trên là số tổ hợp lặp chập 4 của 9 phần tử
). Số tập con thoả tính chất trên là số tổ hợp lặp chập 4 của 9 phần tử
Do đó theo công thức tổ hợp lặp ta có: ![]()
Vậy 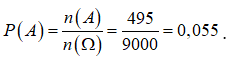
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
12831
Đã trả lời bởi chuyên gia
12831 -
 Đã trả lời bởi chuyên gia
11114
Đã trả lời bởi chuyên gia
11114


