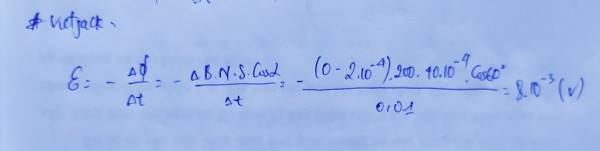Để tính suất điện động cảm ứng trong khung dây, ta dùng định luật Faraday về cảm ứng điện từ. Suất điện động cảm ứng (E\mathcal{E}E) được tính theo công thức:

E=−dΦdt\mathcal{E} = -\frac{d\Phi}{dt}E=−dtdΦ​

Trong đó:

Φ\PhiΦ là từ thông qua khung dây.
dtdtdt là thời gian thay đổi từ thông.
Từ thông (Φ\PhiΦ) được tính bằng công thức:

Φ=B⋅S⋅cos⁡(α)\Phi = B \cdot S \cdot \cos(\alpha)Φ=B⋅S⋅cos(α)

Trong đó:

BBB là cảm ứng từ (B=2×10−4 TB = 2 \times 10^{-4} \, TB=2×10−4T).
SSS là diện tích khung dây (S=40 cm2=40×10−4 m2=4×10−3 m2S = 40 \, cm^2 = 40 \times 10^{-4} \, m^2 = 4 \times 10^{-3} \, m^2S=40cm2=40×10−4m2=4×10−3m2).
α\alphaα là góc giữa vectơ cảm ứng từ và mặt phẳng khung (góc 30∘30^\circ30∘).
Trước khi tính toán, ta cần tinh giá trị từ thông ban đầu (Φ1\Phi_1Φ1​) khi BBB và góc α\alphaα là xác định:

Φ1=B⋅S⋅cos⁡(30∘)\Phi_1 = B \cdot S \cdot \cos(30^\circ)Φ1​=B⋅S⋅cos(30∘)
cos⁡(30∘)=32\cos(30^\circ) = \frac{\sqrt{3}}{2}cos(30∘)=23​​

Thay các giá trị vào công thức:

Φ1=(2×10−4)⋅(4×10−3)⋅32\Phi_1 = (2 \times 10^{-4}) \cdot (4 \times 10^{-3}) \cdot \frac{\sqrt{3}}{2}Φ1​=(2×10−4)⋅(4×10−3)⋅23​​

Tính toán từng bước:
Φ1=(2×4×10−7)⋅32=4×10−7⋅32=23×10−7 Wb\Phi_1 = (2 \times 4 \times 10^{-7}) \cdot \frac{\sqrt{3}}{2} = 4 \times 10^{-7} \cdot \frac{\sqrt{3}}{2} = 2 \sqrt{3} \times 10^{-7} \, WbΦ1​=(2×4×10−7)⋅23​​=4×10−7⋅23​​=23​×10−7Wb

Từ trường giảm từ B=2×10−4 TB = 2 \times 10^{-4} \, TB=2×10−4T đến 0, nên từ thông cuối cùng (Φ2\Phi_2Φ2​) là:

Φ2=0\Phi_2 = 0Φ2​=0

Do đó, sự thay đổi từ thông (dΦd\PhidΦ) là:

dΦ=Φ2−Φ1=0−23×10−7=−23×10−7 Wbd\Phi = \Phi_2 - \Phi_1 = 0 - 2 \sqrt{3} \times 10^{-7} = -2 \sqrt{3} \times 10^{-7} \, WbdΦ=Φ2​−Φ1​=0−23​×10−7=−23​×10−7Wb

Thay vào công thức suất điện động:

E=−dΦdt=−−23×10−70.01=23×10−70.01\mathcal{E} = -\frac{d\Phi}{dt} = -\frac{-2 \sqrt{3} \times 10^{-7}}{0.01} = \frac{2 \sqrt{3} \times 10^{-7}}{0.01}E=−dtdΦ​=−0.01−23​×10−7​=0.0123​×10−7​

Tính giá trị:

E=23×10−5 V\mathcal{E} = 2 \sqrt{3} \times 10^{-5} \, VE=23​×10−5V

Cuối cùng, ta nhân với khoảng 1.732 (giá trị của 3\sqrt{3}3​) để có giá trị thực tế:

E≈2×1.732×10−5≈3.464×10−5 V\mathcal{E} \approx 2 \times 1.732 \times 10^{-5} \approx 3.464 \times 10^{-5} \, VE≈2×1.732×10−5≈3.464×10−5V

Vậy, suất điện động cảm ứng xuất hiện trong khung là khoảng:

E≈3.464×10−5 V≈34.64 μV\mathcal{E} \approx 3.464 \times 10^{-5} \, V \approx 34.64 \, \mu VE≈3.464×10−5V≈34.64μV