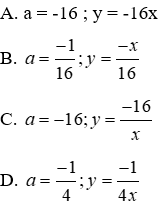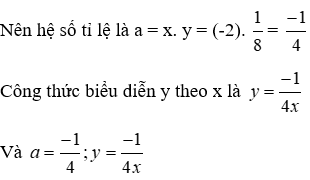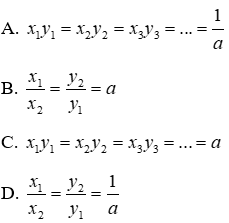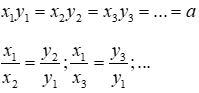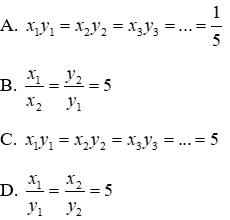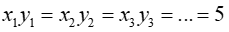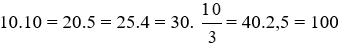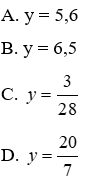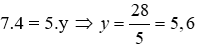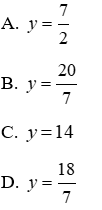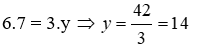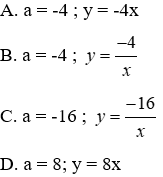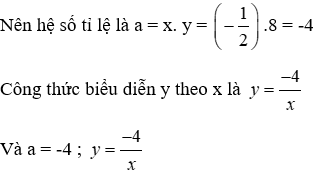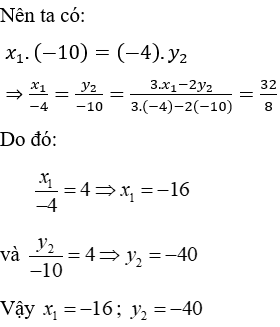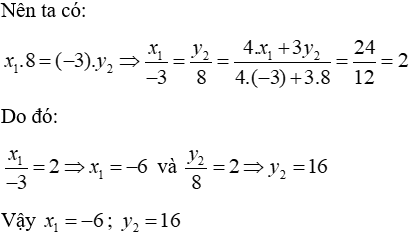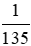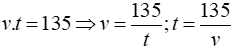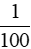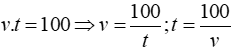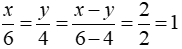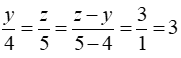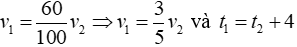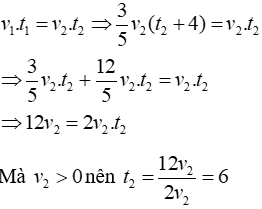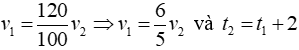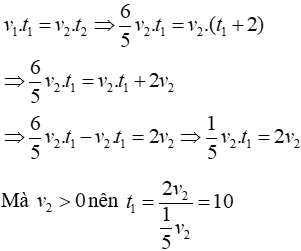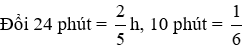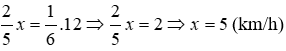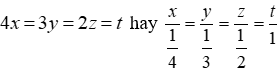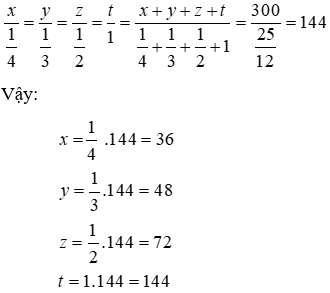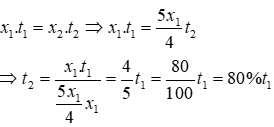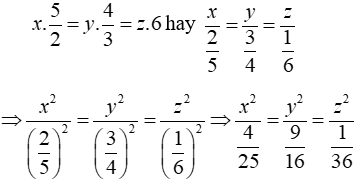Trắc nghiệm Toán học 7 Đại lượng tỉ lệ nghịch

Câu 1: Cho biết x và  là hai đại lượng tỉ lệ nghịchvới nhau. Khi x = -2 và 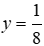. Khi đó hệ số tỉ lệ a và công thức biểu diễn y theo x là

Lời giải:

Vì x và y là hai đai lượng tỉ lê nghịch với nhau và x = -2 thì 

Đáp án cần chọn là: B

Câu 2: Khi 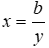 ta nói

A. y tỉ lệ với x

B. y tỉ lệ thuận với x theo hệ số tỉ lệ a

C. y tỉ lệ thuận với x

D, x tỉ lệ thuận với y

Lời giải:

Nếu đại lượng y liên hệ với đại lượng x theo công thức 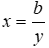  thì ta nói x tỉ lệ nghịch với y theo hệ số tỉ lệ b 

Đáp án cần chọn là: B

Câu 3: Cho x và y là hai đại lượng tỉ lệ nghịch và 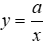. Gọi x¹; x²; x³; ... là các giá trị của x và y¹; y²; y³; ...  là các giá trị tương ứng y. Ta có:

Lời giải:

Nếu hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a thì:

Đáp án cần chọn là: C

Câu 4: Cho x và y là hai đại lượng tỉ lệ nghịch và 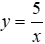. Gọi x¹; x²; x³; ... là các giá trị của x và y¹; y²; y³; ... là các giá trị tương ứng y. Ta có:

Lời giải:

Nếu hai đại lượng y và x tỉ lệ nghịch và 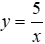 nên hệ số tỉ lệ a = 5, do đó

Đáp án cần chọn là: C

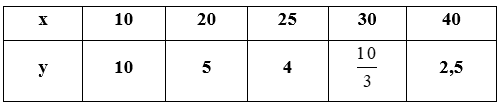
Câu 5: Cho bảng sau:

Khi đó:

A. y tỉ lệ với x

B. y và x là hai đại lượng tỉ lệ thuận

C. y và x là hai đại lượng tỉ lệ nghịch

D. y và x là hai đại lượng bất kì

Lời giải:

Xét các tích giá trị của xx và y,y, ta được:

Nên y và x là hai đại lượng tỉ lệ nghịch.

Đáp án cần chọn là: C

Câu 6: Cho bảng sau:

Khi đó:

A. y tỉ lệ với x

B. y và x là hai đại lượng tỉ lệ thuận

C. y và x là hai đại lượng tỉ lệ nghịch

D. y và x là hai đại lượng bất kì

Lời giải:

Xét các tích giá trị của x và y ta được: 5.2 = (-1).(-10) = 10.1 = 2.5 = 4.2,5 = 10

Nên y và x là hai đại lượng tỉ lệ nghịch.

Đáp án cần chọn là: C

Câu 7: Cho biết x và  là hai đại lượng tỉ lệ nghịch. Khi x = 7 thì y = 4. Tìm y khi x = 5

Lời giải:

Vì x và y là hai đai lượng tỉ lê nghịch nên ta có:

Đáp án cần chọn là: A

Câu 8: Cho biết x và  là hai đại lượng tỉ lệ nghịch. Khi x = 6 thì y = 7. Tìm y khi x = 3

Lời giải:

Vì x và y là hai đai lượng tỉ lê nghịch nên ta có:

Đáp án cần chọn là: C

Câu 9: Cho biết x và y là hai đại lượng tỉ lệ nghịch với nhau. Khi 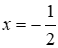 và y = 8. Khi đó hệ số tỉ lệ a và công thức biểu diễn y theo x là

Lời giải:

Vì x và y là hai đai lượng tỉ lê nghịch với nhau và 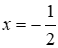 thì y = 8

Đáp án cần chọn là: B

Câu 10: Khi 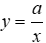 với a ≠ 0 ta nói:

A. y tỉ lệ với x

B. y tỉ lệ thuận với x theo hệ số tỉ lệ a

C. y tỉ lệ thuận với x

D, x tỉ lệ thuận với y

Lời giải:

Nếu đại lượng y liên hệ với đại lượng x theo công thức 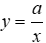  với a ≠ 0 thì ta nói y tỉ lệ nghịch với x  theo hệ số tỉ lệ a. 

Đáp án cần chọn là: B

Câu 11: Cho hai đại lượng tỉ lệ nghịch x và y; x₁, x₂  là hai giá trị của x; y₁,y₂  là hai giá trị tương ứng của y. Biết x₁ = 4, x₂ = 3 và y₁ + y₂ = 14. Khi đó y₂ = ?

A. y₂ = 5

B. y₂ = 7

C. y₂ = 6

D. y₂ = 8

Lời giải:

Với x và y là hai đại lượng tỉ lệ nghịch nên x₁ y₁ = x₂ y₂ mà x₁ = 4, x₂ = 3 và y₁ + y₂ = 14.

Đáp án cần chọn là: D

Câu 12: Cho hai đại lượng tỉ lệ nghịch x và y; x₁, x₂ là hai giá trị của x; y₁, y₂  là hai giá trị tương ứng của y. Biết x₁ = 2, x₂ = 5 và y₁ + y₂ = 21. Khi đó y₁ = ?

A. y₁ = 14

B. y₁ = 6

C. y₁ = 15

D. y₁ = 51

Lời giải:

Với x và y là hai đại lượng tỉ lệ nghịch nên x₁y₁ = x₂y₂ mà x₁ = 2, x₂ = 5 và y₁ + y₂ = 21

Đáp án cần chọn là: C

Câu 13: Cho hai đại lượng tỉ lệ nghịch x và y; x₁, x₂ là hai giá trị của x; y₁, y₂ là hai giá trị tương ứng của y. Biết x₂ = -4; y₁ = -10 và 3x₁ - 2y₂ = 32. Khi đó x₁ và y₂ là?

A. x₁ = 16; y₂ = 40

B. x₁ = -40; y₂ = -16

C. x₁ = 16; y₂ = -40

D. x₁ = -16; y₂ = -40

Lời giải:

Với x và y là hai đại lượng tỉ lệ nghịch nên x₁y₁ = x₂y₂ mà x₂ = -4; y₁ = -10 và 3x₁ - 2y₂ = 32

Đáp án cần chọn là: D

Câu 14: Cho hai đại lượng tỉ lệ nghịch x và y; x₁, x₂ là hai giá trị của x; y₁, y₂ là hai giá trị tương ứng của y. Biết x₂ = -3; y₁ = 8 và 4x₁ + 3y₂ = 24. Khi đó x₁ và y₂ là?

A. x₁ = -6; y₂ = 16

B. x₁ = -6; y₂ = -16

C. x₁ = 16; y₂ = -6

D. x₁ = 6; y₂ = 16

Lời giải:

Với x và y là hai đại lượng tỉ lệ nghịch nên x₁y₁ = x₂y₂ mà  x₂ = -3; y₁ = 8 và 4x₁ + 3y₂ = 24.

Đáp án cần chọn là: A

Câu 15: Một ô tô đi quãng đường 135 km với vận tốc v(km/h) và thời gian t (h). Chọn câu đúng về mối quan hệ của v và t

A. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 

B. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 135

C. v và t là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 135

D. v và t là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 

Lời giải:

Từ bài ra ta có:

Nên v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 135

Đáp án cần chọn là: B

Câu 16: Một ô tô đi quãng đường 100 km với vận tốc v(km/h) và thời gian t (h). Chọn câu đúng về mối quan hệ của v và t

A. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 

B. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 100

C. v và t là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 100

D. v và t là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 

Lời giải:

Từ bài ra ta có:

Nên v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 100

Đáp án cần chọn là: B

Câu 17: Để làm một công việc trong 8 giờ cần 30 công nhân. Nếu có 40 công nhân thì công việc đó được hoàn thành trong mấy giờ?

A. 5 giờ

B. 8 giờ

C. 6 giờ

D. 7 giờ

Lời giải:

Gọi thời gian 40 công nhân làm một công việc đó là x (x >0) (giờ)

Vì số công nhân và thời gian làm của công nhân là hai đại lượng tỉ lệ nghịch, nên theo bài ra ta có:

8.30 = 40 x ⇒ 40x = 240 ⇒ x = 6 giờ.

Vậy 40 công nhân thì công việc đó được hoàn thành trong 6 giờ.

Đáp án cần chọn là: C

Câu 18: Để làm một công việc trong 7 giờ cần 12 công nhân. Nếu có 21 công nhân thì công việc đó được hoàn thành trong mấy giờ?

A. 5 giờ

B. 8 giờ

C. 4 giờ

D. 6 giờ

Lời giải:

Gọi thời gian 21 công nhân làm một công việc đó là x (x >0) (giờ)

Vì cùng một công việc thì số công nhân và thời gian làm của công nhân là hai đại lượng tỉ lệ nghịch, nên theo bài ra ta có:

7.12 = x.21 ⇒ 21x = 84 ⇒ x = 4 giờ.

Vậy 21 công nhân thì công việc đó được hoàn thành trong 44 giờ.

Đáp án cần chọn là: C

Câu 19: Cho biết y tỉ lệ nghịch với x theo tỉ số k_1 (k_1 ≠ 0)  và x tỉ lệ nghịch với z theo tỉ số k_2 (k_2 ≠ 0). Chọn câu đúng

Lời giải:

Đáp án cần chọn là: D

Câu 20: Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ -4 và x tỉ lệ nghịch với z theo hệ số tỉ lệ 3/4. Chọn câu đúng

Lời giải:

Đáp án cần chọn là: C

Câu 21: Một ô tô chạy từ A đến B với vận tốc 50 km/m thì hết 2 giờ 15 phút. Hỏi ô tô chạy từ A đến B với vận tốc 45 km/h thì hết bao nhiêu thời gian?

A. 3,25 giờ

B. 3,5 giờ

C. 3 giờ

D. 2,5 giờ

Lời giải:

Đổi 2 giờ 15 phút = 2,25 giờ

Gọi thời gian ô tô chạy A đến B với vận tốc 45 km/h  là x (x > 0) (giờ)

Vì quãng đường đi không đổi nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.

Theo bài ra ta có: 50.2,25 = 45.x ⇒ 45x = 112,5 ⇒ x = 2,5 giờ.

Vậy thời gian cần tìm là 2,5 giờ.

Đáp án cần chọn là: D

Câu 22: Một ô tô chạy từ A đến B với vận tốc 40 km/m thì hết 3 giờ 30 phút. Hỏi ô tô chạy từ A đến B với vận tốc 35 km/h thì hết bao nhiêu thời gian?

A. 3,25 giờ

B. 4 giờ

C. 3 giờ

D. 2,5 giờ

Lời giải:

Đổi 3 giờ 30 phút = 3,5 giờ

Gọi thời gian ô tô chạy A đến B với vận tốc 35 km/h  là x (x > 0) (giờ)

Vì quãng đường đi không đổi nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.

Theo bài ra ta có: 40.3,5 = 35.x ⇒ 35x = 140 ⇒ x = 4 giờ.

Vậy thời gian cần tìm là 4 giờ.

Đáp án cần chọn là: B

Câu 23: Ba đội máy cày, cày trên ba cánh đồng có diện tích như nhau. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 6 ngày và đội thứ 3 trong 8 ngày. Hỏi đội thứ nhất có bao nhiêu  máy cày, biết rằng đội thứ nhất có hơn đội thứ hai là 2 máy và công suất của các máy như nhau?

A. 10 máy

B. 4 máy

C. 6 máy

D. 8 máy

Lời giải:

Gọi số máy cày của ba đội lần lượt là x; y; z (x; y; z > 0)

Vì diện tích ba cánh đồng là như nhau nên thời gian và số máy cày là hai đại lượng tỉ lệ nghịch

Theo bài ra ta có: x.4 = y.6 = z.8 và x - y = 2

Suy ra: 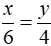. Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

Do đó x = 6 ; y = 4

Vậy đội thứ nhất có 6 máy

Đáp án cần chọn là: C

Câu 24: Ba đội máy cày, cày trên ba cánh đồng có diện tích như nhau. Đội thứ nhất hoàn thành công việc trong4 ngày, đội thứ hai trong 3 ngày và đội thứ 3 trong 4 ngày. Hỏi đội thứ hai có bao nhiêu  máy cày, biết rằng đội thứ hai có ít hơn đội thứ ba là 3 máy và công suất của các máy như nhau?

A. 10 máy

B. 20 máy

C. 12 máy

D. 15 máy

Lời giải:

Gọi số máy cày của ba đội lần lượt là x; y; z (x; y; z > 0)

Vì diện tích ba cánh đồng là như nhau nên thời gian và số máy cày là hai đại lượng tỉ lệ nghịch

Theo bài ra ta có: x.3 = y.5 = z.4 và z - y = 3

Suy ra: 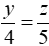. Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

Do đó y = 12 ; z = 15

Vậy đội thứ hai có 12 máy

Đáp án cần chọn là: C

Câu 25: Để làm một công việc trong 12 giờ cần 45 công nhân. Nếu số công nhân tăng thêm 15 người (với năng suất như sau) thì thời gian để hoàn thành công việc giảm đi mấy giờ?

A. 3

B. 6

C. 9

D. 4

Lời giải:

Gọi thời gian để hoàn thành công việc sau khi tăng thêm 15 người là x (0 < x < 12) (giờ)

Từ bài ra ta có số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.

Nếu tăng thêm 15 công nhân thì số công nhân sau khi tăng là 45 + 15 = 60 công nhân

Theo bài ra ta có: 45.12 = 60.x ⇒ 60x = 540 ⇒ x = 9 giờ

Do đó thời gian hoàn thành công việc giảm đi 12 - 9 = 3 giờ

Đáp án cần chọn là: A

Câu 26: Để làm một công việc trong 9 giờ cần 30 công nhân. Nếu số công nhân giảm 12 người (với năng suất như sau) thì thời gian để hoàn thành công việc tăng đi mấy giờ?

A. 15

B. 6

C. 9

D. 4

Lời giải:

Gọi thời gian để hoàn thành công việc sau khi giảm đi 12 người là x (0 < x < 9) (giờ)

Từ bài ra ta có số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.

Nếu giảm đi 12 công nhân thì số công nhân sau khi tăng là 30 - 12 = 18 công nhân

Theo bài ra ta có: 30.9 = 18.x ⇒ 18x = 270 ⇒ x = 15 giờ

Do đó thời gian hoàn thành công việc giảm đi 15 - 9 = 6 giờ

Đáp án cần chọn là: B

Câu 27: Hai xe ô tô cùng từ A đến B. Biết vận tốc của ô tô thứ nhất bằng 60% vận tốc của ô tô thứ hai và thời gian xe thứ nhất đi từ A đến B nhiều hơn thời gian ô tô thứ hai từ A đến B là 4 giờ. Tính thời gian xe thứ hai từ A đến B

A. 3

B. 6

C. 9

D. 4

Lời giải:

Gọi  lần lượt là vận tốc của xe thứ nhất và xe thứ hai (km/h) (v_1; v_2 > 0)

Gọi lần lượt là thời gian của xe thứ nhấy và xe thứ hai (h) (t_1; t_2 > 0)

Từ đề bài ta có:

Vì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên ta có:

Vậy thời gian người thứ hai đi từ A đến B là 6h

Đáp án cần chọn là: B

Câu 28: Hai xe máy cùng từ A đến B. Biết vận tốc của ô tô thứ nhất bằng 120% vận tốc của ô tô thứ hai và thời gian xe thứ nhất đi từ A đến B ít hơn thời gian ô tô thứ hai từ A đến B là 2 giờ. Tính thời gian xe thứ hai từ A đến B

A. 10

B. 12

C. 6

D. 4

Lời giải:

Gọi  lần lượt là vận tốc của xe thứ nhất và xe thứ hai (km/h) (v_1; v_2 > 0)

Gọi lần lượt là thời gian của xe thứ nhấy và xe thứ hai (h) (t_1; t_2 > 0)

Từ đề bài ta có:

Vì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên ta có:

Vậy thời gian người thứ hai đi từ A đến B là t_2 = 10 + 2 = 12 h

Đáp án cần chọn là: B

Câu 29: Cho y thỉ lệ thuận với x theo hệ số tỉ lệ 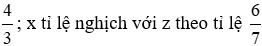. Tìm mối quan hệ giữa y và z

Lời giải:

Đáp án cần chọn là: B

Câu 30: Bạn Mai đi bộ đến trường hết 24 phút, nếu Mai đi xe đạp thì chỉ hết 10 phút. Tính vận tốc khi đi bộ, biết vận tốc đi xe đạp của Mai là 12 km/h

A. 5 km/h

B. 4 km/h

C. 6 km/h

D. 4,5 km/h

Lời giải:

Gọi vận tôc khi đi bộ của Mai là x (x >0) (km/h)

Vì quãng đường đi không đổi nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.

Theo bài ra ta có:

Vậy vận tốc khi đi bộ của Mai là 5 km/h

Đáp án cần chọn là: A

Câu 31: Trước khi xuất khẩu cà phê, người ta chia cà phê thành 4 loại: loại 1, loại 2, loại 3, loại 4 tỉ lệ với 4; 3; 2; 1. Tính khối lượng cà phê loại 4 biết tổng số cà phê bốn loại là 300kg

A. 30 kg

B. 36 kg

C. 48 kg

D. 144 kg

Lời giải:

Gọi x; y; z;t là khối lượng của bốn loại cà phê (kg, 0 < x; y; z;t <300)

Tổng số cà phê bốn loại là 300 kg nên x + y + z + t = 300

Vì khối lượng cà phê loại 1, loại 2, loại 3, loại 4 tỉ lệ nghịch với 4; 3; 2; 1 nên ta có:

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

Khối lượng cà phê loại 4 là 144 kg

Đáp án cần chọn là: D

Câu 32:Trong một cơ sở sản xuất, do cải thiện kĩ thuật nên năng suất công nhân tăng 25% so với ban đầu. Hỏi nếu số công nhân không thay đổi thì thời gian làm việc giảm bao nhiêu phần trăm?

A. 80%

B. 20%

C. 25%

D. 75%

Lời giải:

Gọi thời gian hoàn thành công việc của cơ sở sản xuất ban đầu và sau khi cải tiến kĩ thuật  lần lượt là t_1, t_2 (t_1, t_2 > 0) (giờ), năng suất lao động của công nhân là x₁, x₂ (x₁, x₂ > 0) (sản phẩm/ giờ).

Năng suất lao động của công nhân sau khi cải tiến kĩ thuật là 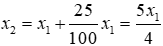 (sản phẩm/ giờ).

Vì năng suất công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên ta có:

Do đó thời gian hoàn thành công việc sau khi cải tiến kĩ thuật bằng 80% thời gian lúc đầu.

Vậy thời gian làm việc sau khi cải tiến kĩ thuật giảm 100%−80%=20%

Đáp án cần chọn là: B

Câu 33:Ba đội công nhân đều làm khối lượng công việc như nhau. Đội 1 làm xong công việc trong 4 ngày, đội thứ hai làm xong công việc trong 6 ngày. Biết rằng, tổng số công nhân dội 1 và đội 2 gấp 5 lần số công nhân đội 3. Hỏi đội 3 làm xonzg công việc trong bao lâu?

A. 25 ngày

B. 20 ngày

C. 12 ngày

D. 10 ngày

Lời giải:

Gọi thời gian hoàn thành công việc của ba đội lần lượt là t_1, t_2, t_3 (t_1, t_2, t_3 > 0) (ngày).

Gọi số công nhân của ba đội lần lượt là x₁, x₂, x_3 (x₁, x₂, x_3 ∈ N*) (người).

Theo đề bài, tổng số công nhân của đội 1 và đội 2 gấp 5 lần số công nhân của đội 3 nên ta có x₁ + x₂ = 5x_3

Vì số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên ta có:

Vậy đội 3 làm xong công việc trong 12 ngày.

Đáp án cần chọn là: C

Câu 34: Một số tự nhiên A được chia ra thành 3 phần tỉ lệ nghịch với các số 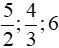. Biết tổng các bình phương của ba phần này là 24309. Tìm số tự nhiên A ban đầu

A. 327

B. 135

C. 273

D. 237

Lời giải:

Gọi ba phần được chia ra từ số A lần lượt là x, y, z (x, y, z > 0)

Theo đề bài, ba phần tỉ lệ nghịch với các số 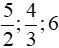 nên ta có:

Tổng bình phương của ba phần là 24309 nên x² + y² + z² = 24309

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

Vậy số tự nhiên A là 237

Đáp án cần chọn là: D