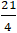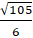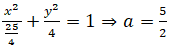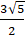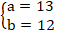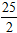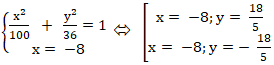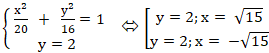Các dạng bài tập về đường Elip chọn lọc, có lời giải

Ví dụ minh họa

Ví dụ 1: Cho elip: 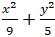 = 1. Có bao nhiêu điểm M thuộc elip sao cho M nhìn hai tiêu điểm dưới một góc 60⁰?

A. 1    B. 2    C. 3    D. 4

Lời giải

+ Ta có; a² = 9; b² = 5 nên c² = a² – b² = 4

⇒ a = 3 và c = 2.

+ Elip có hai tiêu điểm là F₁( - 2; 0) và F₂ ( 2; 0)

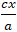
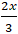
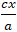
+ Với mọi điểm M ta có: MF₁ = a +  = 3 +  ; MF₂ = a -  = 3 - 

MF₁ + MF₂ = 2a = 6

+ Xét tam giác MF₁F₂; áp dụng định lí cosin ta có:

F₁F₂² = MF₁² + MF₂² – 2. MF₁. MF₂. cosM

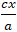
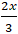
= [ ( MF₁ + MF₂)² - MF₁ = a +  = 3 +  ] – 2.MF₁.MF₂.cos60⁰.

⇔ 4² = 6² – 3.MF₁. MF₂

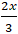
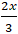
⇔ 16 = 36 - 3. (3 +  ) .( 3 -  )

⇔ 20 = 3. ( 9 - 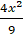 ) ⇔ x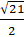² = 

⇔ x = ±  ⇒ y = ± 

Vậy có bốn điểm thỏa mãn là:

Chọn D.

Ví dụ 2: Cho elíp có phương trình 16x² + 25y² = 100.Tính tổng khoảng cách từ điểm thuộc elíp có hoành độ x = 2 đến hai tiêu điểm.

A. √3    B. 2√2    C. 5    D. 4√3

Hướng dẫn giải:

Ta có: 16x² + 25y² = 100 ⇔ 

Tổng khoảng cách từ một điểm bất kì thuộc Elip đến 2 tiêu điểm bằng 2a = 5.

Chọn C.

Ví dụ 3: Cho Elip (E): 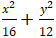 = 1 và điểm M nằm trên (E). Nếu điểm M có hoành độ bằng 1 thì các khoảng cách từ M tới 2 tiêu điểm của (E) bằng

A. 4 ± √2    B. 3 và 5.    C. 3,5 và 4,5 .    D. 4 ± 

Hướng dẫn giải

Ta có a² = 16; b² = 12 nên c² = a² - b² = 4

⇒ a = 4; c = 2 và hai tiêu điểm F₁ ( - 2;0); F₂ (2;0).

Điểm M thuộc (E) và x_M = 1 ⇒ y_M = ± 

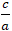
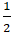
Tâm sai của elip e =  ⇒ e =  .

⇒ MF₁ = a + ex_M = 4,5; MF₂ = a - ex_M = 3,5

Chọn C.

Ví dụ 4: Cho elip (E): 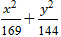 = 1 và điểm M nằm trên (E). Nếu M có hoành độ bằng
- 13 thì khỏang cách từ M đến hai tiêu điểm bằng

A. 10 và 6    B. 8 và 18    C. 13 ± √5    D. 13 ± √10

Hướng dẫn giải

Từ dạng của elip 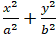 = 1 ta có 

Suy ra: c² = a² – b² = 25 nên c = 5.

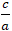
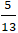
Tâm sai của elip e =  ⇒ e =  .

⇒ MF₁ = a + ex_M = 8; MF₂ = a - ex_M = 18

Chọn B.

Ví dụ 5: Cho elip (E): 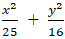 = 1 , với tiêu điểm F₁; F₂. Lấy hai điểm A; B thuộc elip (E) sao cho AF₁ + BF₁ = 8. Khi đó, AF₂ + BF₂ = ?

A. 6    B. 8    C. 12    D. 10

Lời giải

+ Elip ( E): 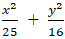 = 1 có a² = 25 nên a = 5

+ Do A ∈( E) nên AF₁ + AF₂ = 2a = 10.

+ Do B ∈( E) nên BF₁ + BF₂ = 2a = 10

⇒ AF₁ + AF₂ + BF₁ + BF₂ = 20

⇔ (AF₁ + BF₁ ) + (AF₂ + BF₂ ) = 20

⇔ 8 + (AF₂ + BF₂ ) = 20

⇔ AF₂ + BF₂ = 12

Chọn C.

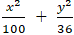
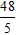
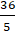
Ví dụ 6: Cho elip (E):  = 1. Qua một tiêu điểm của (E) dựng đường thẳng song song với trục Oy và cắt (E) tại hai điểm M và N. Tính độ dài MN.

A.     B.     C. 25    D. 

Lời giải

+ Xét elip (E): 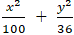 = 1 có:

a² = 100; b² = 36 nên c² = a² – b² = 64

+ Khi đó, Elip có tiêu điểm F₁ ( - 8; 0)

⇒ đường thẳng d// Oy và đi qua F₁ là x = - 8.

+ Giao điểm của d và (E) là nghiệm của hệ phương trình :

Vậy tọa độ hai giao điểm của d và (E) là M( - 8;  ) và N( - 8; -  )

⇒ MN = 

Chọn B.

Ví dụ 7: Cho ( E): 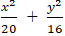 = 1. Một đường thẳng đi qua điểm A(2; 2) và song song với trục hoành cắt (E) tại hai điểm phân biệt M và N. Tính độ dài MN.

A. 3√5    B. 15√2    C. 2√15    D. 5√3

Lời giải

+ Phương trình đường thẳng d: 

⇒ (d) có phương trình là y = 2

+ Ta có d cắt (E) tại M và N nên tọa độ M và N là nghiệm hệ phương trình:

⇒ Tọa độ hai điểm M( √15; 2);N( - √15; 2)

Vậy độ dài đoạn thẳng MN = 2√15 .

Chọn C.

Ví dụ 8: Cho elip: 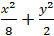 = 1. Hỏi có bao nhiêu điểm thuộc elip có tọa độ nguyên?

A. 1    B. 4    C. 3    D. 8

Lời giải

Nếu điểm M(x; y) thuộc elip thì các điểm A( x; - y) ; B( - x; y) ; C( - x; - y) cũng thuộc elip. Do đó; ta xét điểm M có tọa độ nguyên dương.

Từ 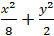 = 1 ⇔ x² = 8 - 4y²

Phương trình trên có nghiệm nếu: 8 - 4y² ≥ 0

Kết hợp x; y > 0 nên 0 < y ≤ √2

⇒ y = 1 và x = 2.

⇒ Các điểm thuộc elip có tọa độ nguyên là: (2;1); (-2; 1); (2; -1) và ( -2; -1)

Chọn B.

Ví dụ 9: Biết Elip (E) có các tiêu điểm F₁( - √7; 0), F₂(√7; 0) và đi qua M(- √7; 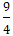 ) . Gọi N là 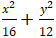điểm đối xứng với M qua gốc toạ độ. Khi đó

A.  = 1    B. OM = 3

C. ON = 3    D. NF₁ + MF₁ = 8.

Hướng dẫn giải:

Ta có N đối xứng với M qua gốc tọa độ nên N(√7; -  ) .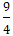

Suy ra: NF₁ = 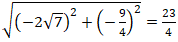 ; MF₁ = 

Từ đó: NF₁ + MF₁ = 8.

Chọn D.