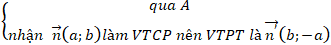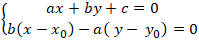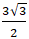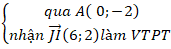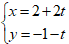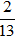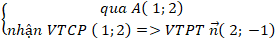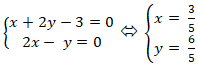A. Phương pháp giải

Cho trước điểm A(x₀; y₀) và phương trình đường thẳng d: ax + by + c = 0 có VTPT
n→( a; b). Tìm hình chiếu của điểm A lên đường thẳng d:

+ Bước 1: Gọi H là hình chiếu của A lên đường thẳng d.

+ Bước 2: Lập phương trình tổng quát của AH

AH: 

⇒ phương trình AH: b(x - x₀) - a(y - y₀) = 0

+ Bước 3: AH và d cắt nhau tại H nên tọa độ điểm H là nghiệm hệ phương trình:

Từ hệ phương trình trên ta suy ra tọa độ điểm H.

• Ví dụ 1: Cho tam giác BAC có AB = 3; BC = 3√3 và góc B = 30⁰.Gọi H là hình chiếu của A lên BC. Tìm mệnh đề đúng?

  A. H nằm trong đoạn BC thỏa mãn: BH = 2 HC

  B. AH =  .

  C. BH = 2.

  D. Tất cả sai

  Lời giải

  + Áp dụng định lí cosin vào tam giác ABC ta có:

  AC² = AB² + BC² – 2.AC.BC.Cos B

  = 3² + (3√3 )² - 2.3.3√3.cos30⁰ = 9

  ⇒ AC = 3 nên AB = AC = 3

  ⇒ Tam giác BAC cân tại A.

  + AH là đường cao nên đồng thời là đường trung tuyến

  ⇒ H là trung điểm của BC: BH = CH = 

  + Xét tam giác vuông AHB có: AH = AB.sinB = 3.sin30⁰ = 1,5.

  Chọn B.

Ví dụ 2: Cho điểm A( 2; 0) và đường thẳng d: x + y - 2 = 0. Tìm hình chiếu của điểm A lên đường thẳng d.

A. ( 2; -1)    B. (2; 0)    C. (1; -2)    D. (-2; -1)

Lời giải

Ta có: 2 + 0 - 2 = 0 nên điểm A thuộc đường thẳng d.

⇒ Hình chiếu của điểm A lên đường thẳng d chính là điểm A.

Chọn B.

Ví dụ 3: Cho tam giác ABC có A( 0; -2).Gọi I ( 2; 4) là trung điểm của AB và J( -4; 2) là trung điểm của AC. Gọi hình chiếu của điểm A lên BC là H. Viết phương trình đường thẳng AH?

A. 6x + 2y - 3 = 0    B. 6x + 2y + 4 =0    C. 2x - y + 1 = 0    D. Tất cả sai

Lời giải

+ Do I và J lần lượt là trung điểm của AB và AC nên IJ là đường trung bình của tam giác ABC ⇒ IJ// BC ( 1) .

+ Do H là hình chiếu của A lên BC

⇒ AH vuông góc BC (2).

Từ(1) và ( 2) suy ra: AH vuông góc IJ

+ Lập phương trình AH: 

⇒ ( AH): 6(x - 0) + 2( y + 2) = 0 hay 6x + 2y + 4 = 0.

Chọn B.

Ví dụ 4: Toạ độ hình chiếu của M(4; 1) trên đường thẳng ∆: x - 2y + 4 = 0 là:

A. ( 14; -19)    B. ( 2; 3)    C. ( ;  )    D. (-  ;  )

Lời giải

+ Đường thẳng ∆ có 1 VTPT n→(1; -2)

Gọi H( 2t - 4; t) là hình chiếu của M trên đường thẳng ∆ thì MH→(2t - 8; t - 1)

⇒ Hai vecto MH→ và n→(2; -3) cùng phương nên:

 ⇒ H( ;  )

Chọn C.

Ví dụ 5: Cho đường thẳng ∆:  và điểm M(3; 3) . Tọa độ hình chiếu vuông góc của M trên đường thẳng ∆ là:

A. (4; -2)    B. (1; 0)    C. (-2; 2)    D. (7; -4)

Lời giải

Gọi H là hình chiếu của M trên ∆.

Ta có: H ∈ ∆ ⇒ H(1 + 3t; - 2t), MH→ = (- 2 + 3t; - 3 - 2t)

Đường thẳng có vectơ chỉ phương là u→( 3; -2) .

Do H là hình chiếu vuông góc của M trên ∆ nên hai đường thẳng MH và ∆ vuông góc với nhau

⇒ MH→.u→ = 0 ⇔ 3( -2 + 3t ) – 2( -3 - 2t) = 0

⇔ -6 + 9t + 6 + 4t = 0 ⇔ 13t = 0 ⇔ t = 0

⇒ H ( 1; 0)

Chọn B.

Ví dụ 6: Tìm hình chiếu của A( 3;-4) lên đường thẳng d: 

A. ( 1; 2)    B. (4; -2)    C. ( -1; 2)    D. ( -1; -3)

Lời giải

+ Lấy điểm H(2 + 2t; -1 - t) thuộc d.

Ta có AH→ = (2t - 1; -t + 3)

Vectơ chỉ phương của d là u→( 2; -1)

+Do H là hình chiếu của A trên d

⇔ AH ⊥ d ⇔ u→.AH→ = 0 ⇔ 2(2t - 1) - (- t + 3) = 0 ⇔ t = 1

+ Với t = 1 ta có H( 4; -2)

Vậy hình chiếu của A trên d là H( 4; -2).

Chọn B.

Ví dụ 7: Cho đường thẳng ∆:  . Hoành độ hình chiếu của M( 4; 5) trên ∆ gần nhất với số nào sau đây ?

A. 1,1    B. 1,2    C. 1,3    D. 1,5

Lời giải

Gọi H là hình chiếu của M trên ∆.

Ta có: H ∈ ∆ nên H( 2 - 3t; 1 + 2t) và MH→( -2 - 3t; -4 + 2t)

Đường thẳng ∆có vectơ chỉ phương là u→(3; - 2) .

u→ ⊥ MH→ ⇔ u→.MH→ = 0 ⇔ 3(-2 - 3t) - 2(-4 + 2t) = 0 ⇔ -13t + 2 = 0 ⇔ t = 
⇒ H( ;  )

⇒ Hoành độ của điểm H là  .

Chọn D.

Ví dụ 8: Cho điểm A( 1; 2) và đường thẳng (d): x + 2y - 3 = 0 .Tìm hình chiếu của A lên đường thẳng d.

A. ( 1; -2)    B. (-  ;  )    C. (  ;  )    D. Đáp án khác

Lời giải

+ Gọi H là hình chiếu của A lên đường thẳng (d) .

+ Lập phương trình đường thẳng AH:

(AH) : 

⇒ Phương trình ( AH) : 2(x - 1) – 1.( y - 2) = 0 hay 2x - y = 0

+ Hai đường thẳng AH và d cắt nhau tại H nên tọa độ điểm H là nghiệm hệ phương trình:

Chọn C.