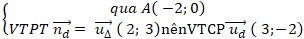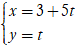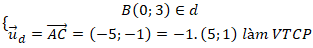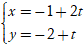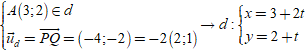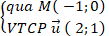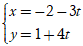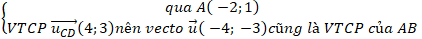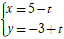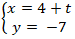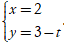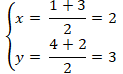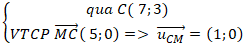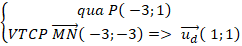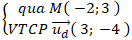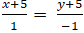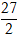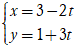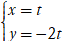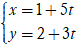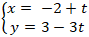B. Ví dụ minh họa

• Ví dụ 1: Cho hai đường thẳng d và ∆ vuông góc với nhau.Biết đường thẳng
  ∆:  và điểm A( -2; 0) thuộc đường thẳng d. Viết phương trình chính tắc của đường thẳng d.

  A. 2x + 3y + 4 = 0    B.     C.     D. Đáp án khác

  Lời giải

  + Đường thẳng ∆ nhận vecto u_∆→( 2; 3) làm VTCP.

  + Do đường thẳng d vuông góc đường thẳng ∆ nên :

  (d): 

  ⇒ Phương trình chính tắc của đường thẳng d: 

  Chọn C.

Ví dụ 2. Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(2; 0); B( 0; 3)và C( -3;-1). Đường thẳng đi qua điểm B và song song với AC có phương trình tham số là:

A.     B.     C.     D. 

Lời giải

Gọi d là đường thẳng qua B và song song với AC. Ta có

Đường thẳng (d): 

nên d:  (t ∈ R)

Chọn A.

Ví dụ 3. Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(3; 2); P(4; 0) và Q(0; -2). Đường thẳng đi qua điểm A và song song với PQ có phương trình tham số là:

A.     B.     C.     D. 

Lời giải

+ Gọi d là đường thẳng qua A và song song với PQ.

Ta có: 

+ Cho t= -2 ta được điểm M (-1; 0) thuộc d.

Đường thẳng (d): 

⇒ Phương trình tham số của đường thẳng d: 

Chọn C.

Ví dụ 4. Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có đỉnh
A(-2; 1)và phương trình đường thẳng chứa cạnh CD là  . Viết phương trình tham số của đường thẳng chứa cạnh AB.

A.     B.     C.     D. 

Lời giải

Do ABCD là hình bình hành nên AB//CD

⇒ Đường thẳng AB: 

⇒ Phương trình tham số của AB: 

Chọn B.

Ví dụ 5. Viết phương trình tham số của đường thẳng d đi qua điểm M(-3; 5) và song song với đường phân giác của góc phần tư thứ nhất.

A.     B.     C.     D. 

Lời giải

Phương trình đường phân giác góc phần tư (I) : x - y = 0

Đường thẳng này nhận VTPT là n→(1 ; -1) và nhận VTCP u→(1 ;1)

Đường thẳng d song song với đường phân giác góc phần tư thứ nhất nên d nhận u→(1 ;1) làm VTCP.

⇒ Phương trình tham số của đường thẳng d: 

Chọn B.

Ví dụ 7. Viết phương trình tham số của đường thẳng d đi qua điểm M(4; -7) và song song với trục Ox.

A.     B.     C.     D. 

Lời giải

Phương trình trục Ox là y = 0. Đường thẳng này nhận vecto n→( 0 ;1) làm VTPT và vecto u→(1 ; 0) làm VTCP.

Do đường thẳng d// Ox nên đường thẳng d nhận u→(1 ;0) làm VTCP.

⇒ Phương trình tham số của đường thẳng d là :

Chọn D.

Ví dụ 8. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(1 ; 4); B( 3; 2) và C( 7; 3). Viết phương trình tham số của đường trung tuyến CM của tam giác.

A.     B.     C.     D. 

Lời giải

Do M là trung điểm của AB nên tọa độ của điểm M là:

Đường trung tuyến CM: 

⇒ Phương trình tham số của CM: 

Chọn C.

Ví dụ 9: Cho tam giác ABC có M, N và P lần lượt là trung điểm của AB; BC và AC. Viết phương trình tham số của đường thẳng AC biết M(1; 3); N( - 2; 0) và P( -3; 1)?

A.     B.     C.     D. Tất cả sai

Lời giải

Do M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC.

⇒ MN// AC.

Đường thẳng AC: 

⇒ Phương trình tham số của đường thẳng AC: 

Chọn A.

Ví dụ 10: Phương trình tham số của đường thẳng (d) đi qua điểm M( -2; 3) và vuông góc với đường thẳng (d’) : 3x - 4y + 1 = 0 là:

A.     B.     C.     D. 4x + 3y - 1 = 0 .

Lời giải

Ta có (d) ⊥ (d'): 3x - 4y + 1 = 0 ⇒ VTCP u_d→ = (3; -4)

Đường thẳng (d) : 

Suy ra  (t ∈ R)

Chọn B.

C. Bài tập vận dụng

• Câu 1: Viết phương trình của đường thẳng d đi qua điểm M(6; -10) và vuông góc với trục Oy.

  A. y + 10 = 0 .    B. x – 6 = 0.    C. x + y = -4    D. y - 10 

Câu 2: Cho hai đường thẳng (a): x + y - 2 = 0 và ( b): 2x + 3y - 5. Viết phương trình tham số của đường thẳng (d) đi qua giao điểm của hai đường thẳng (a); (b) đồng thời đường thẳng d song song với đường thẳng (a)?

A.     B.     C.     D. Đáp án khác

Câu 3: Cho tam giác ABC cân tại A có phương trình đường thẳng BC: x + y - 10 = 0. Biết điểm M(5;5) là trung điểm của BC. Viết phương trình chính tắc đường trung tuyến xuất phát từ A của tam giác ABC?

A.     B.     C.     D. 

Câu 4: Đường thẳng d đi qua điểm M(0; -2) và có vectơ chỉ phương u→ = ( 3; 0) có phương trình tổng quát là:

A. d: x = 0    B. d: y + 2 = 0    C. d: y - 2 = 0    D. d: x – 2 = 0

Câu 5: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2; 4); B( 5; 0) và
C( 2; 1). Trung tuyến BM của tam giác đi qua điểm N có hoành độ bằng 20 thì tung độ bằng:

A. - 12    B. -     C. - 13    D. - 

Câu 6: Đường thẳng d đi qua điểm M(-1 ; 2) và vuông góc với đường thẳng
∆ : 2x + y - 3 = 0 có phương trình tổng quát là:

A. 2x + y - 7 = 0    B. x - 2y + 4 = 0    C. x + 2y = 0    D. x - 2y + 5 = 0.

Câu 7: Viết phương trình đường thẳng ∆ đi qua điểm A( 2;-3) và song song với đường thẳng d : 

A. 2x - 3y = 0    B. 3x + 2y = 0    C. 2x + 3y + 1 = 0    D. 3x - 2y = 0

Câu 8: Cho tam giác ABC có A(1;2) ;B( 3;0) và C( 2; -4) . Đường thẳng d đi qua B và song song với AC có phương trình tổng quát là:

A. x - 6y - 3 = 0    B. x + 6y - 3 = 0    C. 6x + y – 18 = 0    D. Đáp án khác

Câu 9: Viết phương trình tổng quát của đường thẳng d đi qua điểm M( -1; 0) và vuông góc với đường thẳng ∆ : 

A. 2x + y + 2 = 0.    B. 2x - y + 2 = 0.    C. x - 2y + 1 = 0.    D. x + 2y + 1 = 0.

Câu 10: Đường thẳng d đi qua điểm M( -2; 1) và vuông góc với đường thẳng
∆ :  có phương trình tham số là:

A.     B.     C.     D. 

Câu 11: Viết phương trình tổng quát của đường thẳng d đi qua điểm M(3; -1) và vuông góc với đường phân giác góc phần tư thứ hai.

A. x + y - 4 = 0    B. x - y - 4 = 0    C. x + y + 4 = 0    D. x - y + 4 = 0

Câu 12: Viết phương trình tham số của đường thẳng d đi qua M( -2; 3) và vuông góc với đường thẳng ∆: x - 3y = 0.

A. x - 3y + 1 = 0    B.     C.     D.