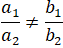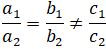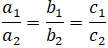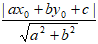1. Vectơ pháp tuyến của đường thẳng

+ Vectơ n→ ≠ 0→ gọi là vectơ pháp tuyến (VTPT) của ∆ nếu giá của nó vuông góc với ∆.

Nhận xét : Nếu n→ là VTPT của ∆ thì k.n→(k ≠ 0) cũng là VTPT của ∆.

+ Trong mặt phẳng tọa độ; mọi đường thẳng đều có phương trình tổng quát dạng:

    ax + by + c = 0 với a² + b² > 0.

+ Các dạng đặc biệt của phương trình tổng quát:

    - Đường thẳng by + c = 0 song song hoặc trùng với trục Ox.

    - Đường thẳng ax + c = 0 song song hoặc trùng với trục Oy.

    - Đường thẳng ax + by = 0 đi qua gốc tọa độ.

+ Đường thẳng có phương trình: 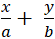 = 1 ( a ≠ 0; b ≠ 0) đi qua hai điểm A(a; 0) và B(0; b)

Phương trình trên được gọi là phương trình đường thẳng theo đoạn chắn.

+ Xét đường thẳng ∆ có phương trình tổng quát: ax + by + c= 0

   Nếu b ≠ 0 thì phương trình trên được đưa về dạng: y= kx + m ( *)

   Khi đó k được gọi là hệ số góc của đường thẳng ∆ và ( *) gọi là phương trình của ∆ theo hệ số góc.

2. Vị trí tương đối của hai đường thẳng

Cho hai đường thẳng : ∆₁ = a₁x + b₁y + c₁ = 0 ; ∆₂ = a₂x + b₂y + c₂ = 0

Để xét vị trí tương đối của hai đường thẳng ∆₁ , ∆₂ ta xét số nghiệm của hệ phương trình

 (I)

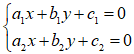
Chú ý: Nếu a₂b₂c₂ ≠ 0 thì :

∆₁ cắt ∆₂ ⇔ 

∆₁ song song ∆₂ ⇔ 

∆₁ trùng ∆₂ ⇔ 

1. Vectơ chỉ phương của đường thẳng

Vectơ u→ ≠ 0→ được gọi là vectơ chỉ phương (VTCP) của đường thẳng ∆ nếu giá của nó song song hoặc trùng với ∆.

Nhận xét : Nếu u→ là VTCP của ∆ thì k.u→( k ≠0) cũng là VTCP của ∆.

2. Phương trình tham số của đường thẳng

Cho đường thẳng ∆ đi qua M₀ (x₀; y₀) và u→( a; b) là VTCP. Khi đó phương trình tham số của đường thẳng có dạng:

 ( 1)

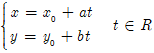
Hệ ( 1) được gọi là phương trình tham số của đường thẳng ∆, với tham số t.

3. Phương trình chính tắc của đường thẳng

Cho đường thẳng ∆ đi qua M₀ (x₀; y₀) và u→(a;b) (với a ≠ 0, b ≠ 0 ) là VTCP. Khi đó phương trình chính tắc của đường thẳng có dạng:

 (2)

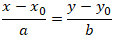
Phương trình ( 2) được gọi là phương trình chính tắc của đường thẳng.

Nếu a = 0 hoặc b = 0 thì đường thẳng không có phương trình chính tắc.

4. Liên hệ giữa VTCP và VTPT

VTPT và VTCP vuông góc với nhau. Do đó nếu ∆ có VTCP u→( a; b) thì n→( b; -a) là một VTPT của ∆.

5. Khoảng cách từ một điểm đến một đường thẳng.

Khoảng cách từ một điểm M(x₀; y₀) đến đường thẳng ∆: ax + by + c = 0 cho bởi công thức:

    d(M₀, ∆) = 

6. Vị trí của hai điểm đối với một đường thẳng.

Cho đường thẳng ∆: ax + by + c = 0 và hai điểm M(x_M; y_M); N(x_N; y_N) không nằm trên ∆. Khi đó:

    + Hai điểm M và N cùng phía so với ∆ khi và chỉ khi:

       ( ax_M + by_M + c).( ax_N + by_N + c) > 0.

    + Hai điểm M và N khác phía so với ∆ khi và chỉ khi:

       ( ax_M + by_M + c).(ax_N + by_N + c) < 0.

7. Góc giữa hai đường thẳng.

+ Định nghĩa: Hai đường thẳng a và b cắt nhau tạo thành bốn góc. Số đo nhỏ nhất của các góc đó được gọi là số đo của góc giữa hai đường thẳng a và b.

Khi a song song hoặc trùng với b, ta quy ước góc giữa chúng là 0⁰.

Kí hiệu: (a;b)

+ Góc giữa hai đường thẳng không vượt quá 90⁰ nên ta có:

   (a; b) = ( u→; v→) nếu ( u→; v→) ≤ 90⁰

    (a; b) = 180⁰ - ( u→; v→) nếu ( u→; v→) > 90⁰

    Trong đó; u→ và v→ lần lượt là VTCP của a và b.

+ Góc giữa hai đường thẳng Δ₁ và Δ₂ có VTPT n₁→ = (a₁; b₁) và n₂→ = (a₂; b₂) được tính theo công thức:

cos(Δ₁, Δ₂) = cos(n₁→, n₂→) =