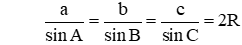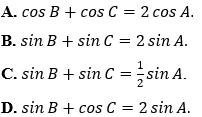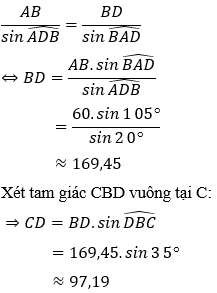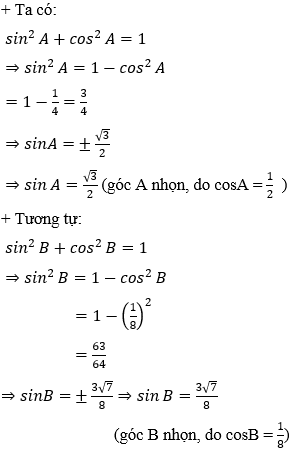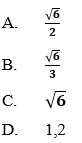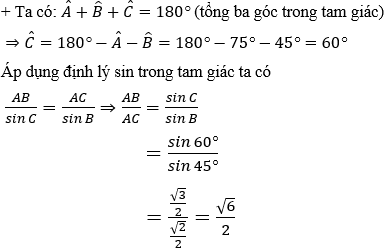Cách giải bài tập về Định lí Sin trong tam giác cực hay, chi tiết
Cách giải bài tập về Định lí Sin trong tam giác cực hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách giải bài tập về Định lí Sin trong tam giác cực hay, chi tiết
Cách giải bài tập về Định lí Sin trong tam giác cực hay, chi tiết
A. Phương pháp giải
Sử dụng định lý sin để giải bài tập.
Định lý sin trong tam giác:
Cho tam giác ABC có BC = a, CA = b, AB = c và có R bán kính đường tròn ngoại tiếp tam giác ABC
Khi đó ta có:
B. Ví dụ minh họa
Ví dụ 1: Cho tam giác ABC với BC = a, CA = b và AB = c thỏa mãn b + c = 2a. Đẳng thức nào sau đây đúng?
Hướng dẫn giải:
Đáp án B
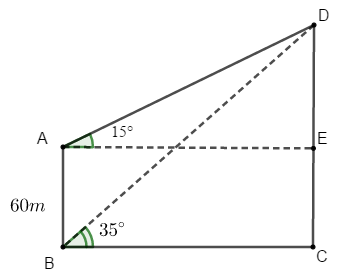
Ví dụ 2: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60m.
Hướng dẫn giải:
Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.
Áp dụng định lý sin trong tam giác ABD ta có:
Vậy ngọn núi cao xấp xỉ bằng 97,19 m.
Ví dụ 3: Cho tam giác ABC có BC = 8, cosA = 1/2 và cosB = 1/8. Tính cạnh AC.
Hướng dẫn giải:
Ví dụ 4: Cho tam giác 
Hướng dẫn giải:
Đáp án A
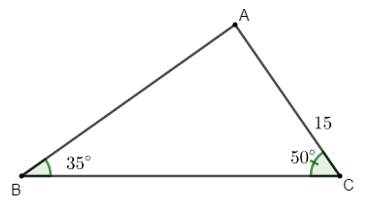
Ví dụ 5: Cho tam giác ABC có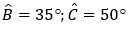 
và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC.
Hướng dẫn giải:
Bài viết liên quan
- Tìm m để góc giữa hai vecto bằng một số cho trước (45 độ, góc nhọn, góc tù) cực hay
- Cách giải bài tập về Định lí Cô-sin trong tam giác cực hay, chi tiết
- Công thức, cách tính độ dài đường trung tuyến cực hay, chi tiết
- Công thức, cách tính Diện tích tam giác cực hay, chi tiết
- Bài tập Công thức Heron tính diện tích tam giác cực hay, chi tiết
