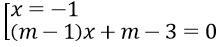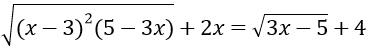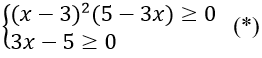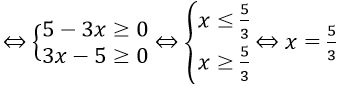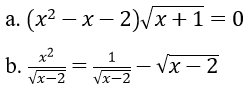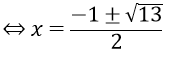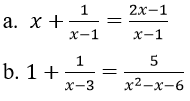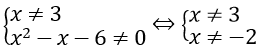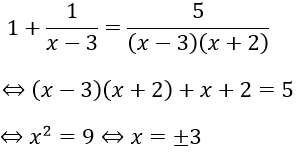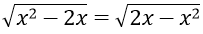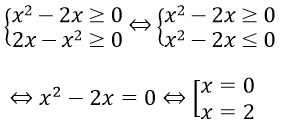Lý thuyết & Phương pháp giải

- Phương trình tương đương: Hai phương trình f₁(x) = g₁(x) và f₂(x) = g₂(x) được gọi là tương đương nếu chúng có cùng tập nghiệm

- Kí hiệu là f₁(x) = g₁(x) ⇔ f₂(x) = g₂(x)

- Phép biến đổi không làm thay đổi tập nghiệm của phương trình gọi là phép biến đổi tương đương.

- Phương trình hệ quả: f₂(x) = g₂(x) gọi là phương trình hệ quả của phương trình f₁(x) = g₁(x) nếu tập nghiệm của nó chứa tập nghiệm của phương trình f₁(x) = g₁(x)

- Kí hiệu là f₁(x) = g₁(x) ⇒ f₂(x) = g₂(x)

- Để giải phương trình ta thực hiện các phép biến đổi để đưa về phương trình tương đương với phương trình đã cho đơn giản hơn trong việc giải nó. Một số phép biến đổi thường sử dụng:

   + Cộng (trừ) cả hai vế của phương trình mà không làm thay đổi điều kiện xác định của phương trình ta thu được phương trình tương đương phương trình đã cho.

   + Nhân (chia) vào hai vế với một biểu thức khác không và không làm thay đổi điều kiện xác định của phương trình ta thu được phương trình tương đương với phương trình đã cho.

   + Bình phương hai vế của phương trình ta thu được phương trình hệ quả của phương trình đã cho.

Bình phương hai vế của phương trình (hai vế luôn cùng dấu) ta thu được phương trình tương đương với phương trình đã cho.

Ví dụ minh họa

Bài 1: Tìm m để cặp phương trình sau tương đương

x² + mx - 1 = 0  (1) và (m-1)x² + 2(m-2)x + m - 3 = 0   (2)

Hướng dẫn:

Giả sử hai phương trình (1) và (2) tương đương

Ta có (m-1)x² + 2(m-2)x + m - 3 = 0

⇔ 

Do hai phương trình tương đương nên x = -1 cũng là nghiệm của phương trình  (1)

Thay x = -1 vào phương trình (1) ta được m = 0

Với m = 0 thay vào hai phương trình ta thấy không tương đương.

Vậy không có giá trị nào của m thỏa mãn.

Bài 2: Giải phương trình

Hướng dẫn:

Điều kiện:

Ta thấy x = 3 thỏa mãn điều kiện (*)

Nếu x ≠ 3. thì (*)

Do đó điều kiện xác định của phương trình là x = 3 hoặc x = 5/3

Thay x = 3 và x = 5/3 vào phương trình thấy chỉ có x = 3 thỏa mãn

Vậy phương trình đã cho có nghiệm duy nhất S = {3}

Bài 3: Giải phương trình

Hướng dẫn:

a. Điều kiện: x ≥ -1.

Ta có x = -1 là một nghiệm.

Nếu x > -1 thì √(x+1) > 0. Do đó phương trình tương đương

x² - x - 2 = 0 ⇔ x = -1 hoặc x = 2.

Đối chiếu điều kiện ta được nghiệm của phương trình là x = -1, x = 2.

Vậy phương trình đã cho có hai nghiệm S = {-1; 2}

b. ĐKXĐ: x > 2

Với điều kiện đó phương trình tương đương với phương trình

x² = 1 - (x - 2)⇔ x² + x - 3 = 0

Đối chiếu với điều kiện ta thấy không có giá trị nào thỏa mãn

Vậy phương trình vô nghiệm

Hướng dẫn:

a. Điều kiện: x ≠ 1.

Với điều kiện trên phương trình tương đương x² - x + 1 = 2x - 1 ⇔ x = 1 hoặc x = 2

Đối chiếu điều kiện ta được phương trình có nghiệm duy nhất x = 2.

b. ĐKXĐ : 

Với điều kiện đó phương trình tương đương với

Đối chiếu với điều kiện ta có nghiệm của phương trình là x = -3

Bài 5: Giải phương trình

Hướng dẫn:

Điều kiện:

Thử lại ta thấy cả x = 0 và x = 2 đều thỏa mãn phương trình

Vậy tập nghiệm của phương trình là S = {0;2}