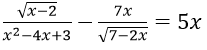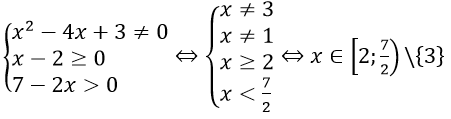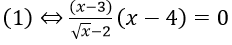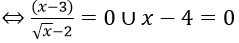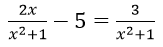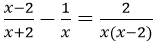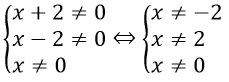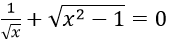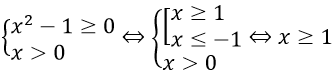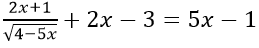Lý thuyết & Phương pháp giải

1. Khái niệm phương trình một ẩn

Cho hai hàm số y = f(x) và y = g(x) có tập xác định lần lượt là D_f và D_g.

Đặt D = D_f ∩ D_g. Mệnh đề chứa biến "f(x) = g(x)" được gọi là phương trình một ẩn, x gọi là ẩn và D gọi tập xác định của phương trình.

Số x₀ ∈ D gọi là một nghiệm của phương trình f(x) = g(x) nếu "f(x_o) = g(x_o)" là một mệnh đề đúng.

2. Phương trình tương đương

Hai phương trình gọi là tương đương nếu chúng có cùng một tập nghiệm. Nếu phương trình f₁(x) = g₁(x) tương đương với phương trình f₂(x) = g₂(x) thì viết

f₁(x) = g₁(x) ⇔ f₂(x) = g₂(x)

Định lý 1: Cho phương trình f(x) = g(x) có tập xác định D và y = h(x) là một hàm số xác định trên D. Khi đó trên miền D, phương trình đã cho tương đương với mỗi phương trình sau:

    (1): f(x) + h(x) = g(x) + h(x)

    (2): f(x).h(x) = g(x).h(x) với h(x) ≠ 0, ∀x ∈ D.

3. Phương trình hệ quả

Phương trình f₁(x) = g₁(x) có tập nghiệm là S₁ được gọi là phương trình hệ quả của phương trình f₂(x) = g₂(x) có tập nghiệm S₂ nếu S₁ ⊂ S₂.

Khi đó viết:

f₁(x) = g₁(x) ⇒ f₂(x) = g₂(x)

Định lý 2: Khi bình phương hai vế của một phương trình, ta được phương trình hệ quả của phương trình đã cho: f(x) = g(x) ⇒ [f(x)]² = [g(x)]².

Lưu ý:

    + Nếu hai vế của 1 phương trình luôn cùng dấu thì khi bình phương 2 vế của nó, ta được một phương trình tương đương.

    + Nếu phép biến đổi tương đương dẫn đến phương trình hệ quả, ta phải thử lại các nghiệm tìm được vào phương trình đã cho để phát hiện và loại bỏ nghiệm ngoại lai.

4. Phương pháp giải tìm tập xác định của phương trình

- Điều kiện xác định của phương trình bao gồm các điều kiện để giá trị của f(x), g(x) cùng được xác định và các điều kiện khác (nếu có yêu cầu trong đề bài).

- Điều kiện để biểu thức

    +  √(f(x)) xác định là f(x) ≥ 0

    +  1/f(x) xác định là f(x) ≠ 0

    +  1/√(f(x)) xác định là f(x) > 0

Ví dụ minh họa

Bài 1: Tìm điều kiện xác định của phương trình

Hướng dẫn:

Điều kiện xác định:

Vậy TXĐ: D = [2; 7/2)\{3}

Bài 2: Khi giải phương trình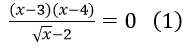một học sinh tiến hành theo các bước sau:

Bước 1:

Bước 2:

Bước 3: ⇔ x = 3 ∪ x = 4

Bước 4: Vậy phương trình có tập nghiệm là: T = {3; 4}

Cách giải trên sai từ bước nào?

Hướng dẫn:

Vì biến đổi tương đương mà chưa đặt điều kiên nên sai ở bước 2.

Bài 3: Tìm tập xác định của phương trình

Hướng dẫn:

Điều kiện xác định: x² + 1 ≠ 0 (luôn đúng)

Vậy TXĐ: D = R.

Bài 4: Tìm tập xác định của phương trình

Hướng dẫn:

Điều kiện xác định:

Vậy TXĐ: R\{-2; 0; 2}

Bài 5: Tìm tập xác định của phương trình

Hướng dẫn:

Điều kiện xác định:

Bài 6: Tìm điều kiện xác định của phương trình

Hướng dẫn:

Điều kiện xác định: 4 - 5x > 0 ⇔ x < 4/5 (luôn đúng)

Vậy TXĐ: D = (-∞; 4/5)

Bài 7: Khi giải phương trình √(x² - 5) = 2 - x  (1), một học sinh tiến hành theo các bước sau:

Bước 1: Bình phương hai vế của phương trình (1) ta được:

x² - 5 = (2 - x)²     (2)

Bước 2: Khai triển và rút gọn (2) ta được 4x = 9

Bước 3: (2) ⇔ x = 9/4

Vậy phương trình có một nghiệm là x = 9/4

Cách giải trên đúng hay sai? Nếu sai thì sai ở bước nào?

Hướng dẫn:

Vì phương trình (2) là phương trình hệ quả nên ta cần thay nghiệm x = 9/4 vào phương trình (1) để thử lại. Nên sai ở bước thứ 3.