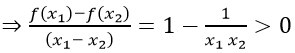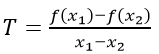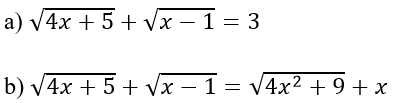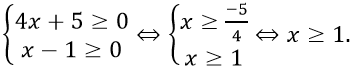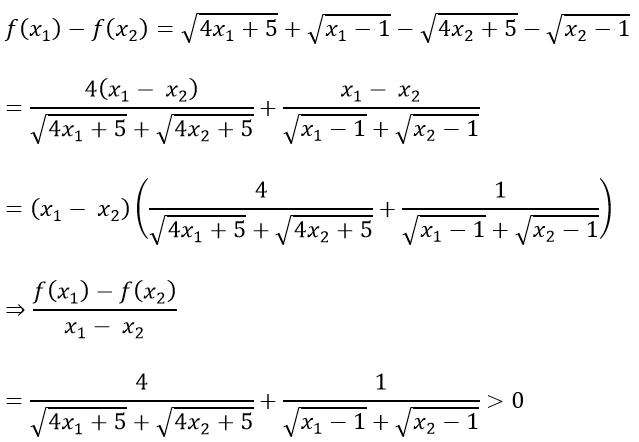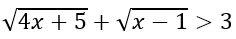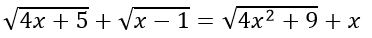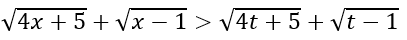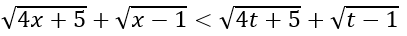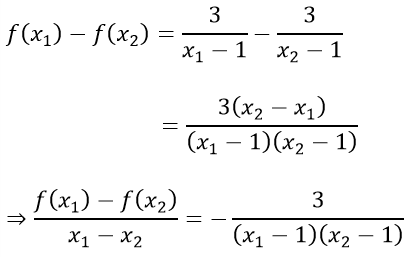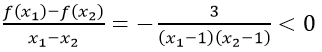1. Phương pháp giải.

C1: Cho hàm số y = f(x) xác định trên K. Lấy x₁; x₂ ∈ K;x₁ < x₂, đặt T = f(x₁ )-f(x₂ )

    + Hàm số đồng biến trên K ⇔ T > 0.

    + Hàm số nghịch biến trên K ⇔ T < 0.

C2: Cho hàm số y = f(x) xác định trên K. Lấy x₁; x₂ ∈ K;x₁ ≠ x₂, đặt 

    + Hàm số đồng biến trên K ⇔ T > 0.

    + Hàm số nghịch biến trên K ⇔ T < 0.

2. Các ví dụ minh họa.

Ví dụ 1: Cho hàm số y = f(x) = x² - 4

a) Xét chiều biến thiên cuả hàm số trên (- ∞;0) và trên (0;+ ∞)

b) Lập bảng biến thiên của hàm số trên [-1;3] từ đó xác định giá trị lớn nhất, nhỏ nhất của hàm số trên[-1;3].

Hướng dẫn:

TXĐ: D = R.

a) ∀ x₁; x₂ ∈ R; x₁ < x₂ ⇒ x₂ - x₁ > 0

Ta có T = f(x₂ ) - f(x₁ )=(x₂² - 4) - (x₁² - 4) = (x₂ - x₁ )(x₂ + x₁ )

Nếu x₁; x₂ ∈ (- ∞;0) thì T < 0. Vậy hàm số y=f(x) nghịch biến trên (- ∞;0).

Nếu x₁; x₂ ∈ (0; + ∞) thì T > 0. Vậy hàm số y = f(x) đồng biến trên (0; + ∞).

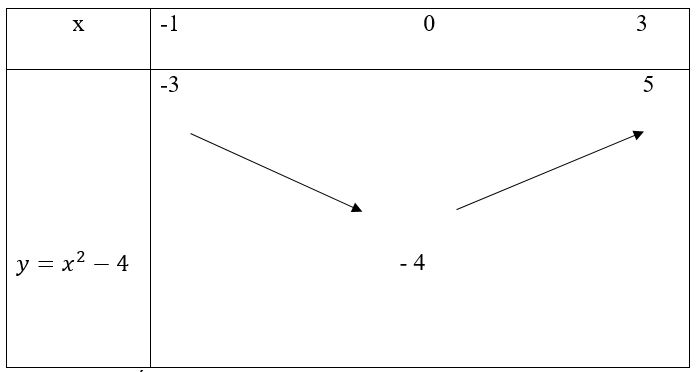
b) Bảng biến thiên của hàm số y = f(x) = x² - 4 trên [-1; 3]

Dựa vào bảng biến thiên ta có:

Giá trị lớn nhất của hàm số trên [-1; 3] là 5, đạt được khi x = 3.

Giá trị nhỏ nhất của hàm số trên [-1; 3] là – 4, đạt được khi x = 0.

Ví dụ 2: Xét sự biến thiên của hàm số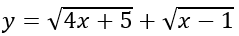trên tập xác định của nó.

Áp dụng tìm số nghiệm của các phương trình sau:

Hướng dẫn:

ĐKXĐ:

Suy ra TXĐ: D = [1; + ∞)

Với mọi x₁; x₂ ∈ [1; + ∞), x₁ ≠ x₂, ta có:

Nên hàm số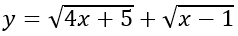đồng biến trên khoảng [1; + ∞).

a) Vì hàm số đã cho đồng biến trên [1; + ∞) nên

Nếu x > 1 ⇒ f(x) > f(1) hay

Suy ra phương trình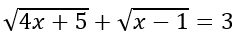không có nghiệm x > 1.

Với x = 1 dễ thấy nó là nghiệm của phương trình đã cho

Vậy phương trình có nghiệm duy nhất x = 1.

b)

ĐKXĐ: x ≥ 1

Đặt x² + 1 = t, t ≥ 1 ⇒ x² = t - 1

Do x ≥ 1 nên x = √(t-1). Khi đó phương trình trở thành:

⇔ f(x)=f(t)

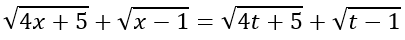
Nếu x > t ⇒ f(x) > f(t) hay

Suy ra phương trình đã cho không có nghiệm thỏa mãn x > t.

Nếu x < t ⇒ f(x)< f(t) hay

Suy ra phương trình đã cho không có nghiệm thỏa mãn x < t.

Vậy f(x) = f(t) ⇔ x = t hay x² + 1 = x ⇔ x² - x + 1 = 0 (vô nghiệm)

Vậy phương trình đã cho vô nghiệm.

Nhận xét:

Hàm số y = f(x) đồng biến (hoặc nghịch biến) trên toàn bộ tập xác định thì phương trình f(x)=0 có tối đa một nghiệm.

Nếu hàm số y = f(x) đồng biến (nghịch biến) trên D thì f(x) > f(y) ⇔ x > y (x < y) và f(x) = f(y) ⇔ x = y ∀ x,y ∈ D. Tính chất này được sử dụng nhiều trong các bài toán đại số như giải phương trình , bất phương trình , hệ phương trình và các bài toán cực trị.

Ví dụ 3: Xét sự biến thiên của hàm số sau trên khoảng (1; + ∞)

a) y = 3/(x-1)

b) y = x + 1/x

Hướng dẫn:

a) Với mọi x₁; x₂ ∈ (1; + ∞); x₁ ≠ x₂ ta có:

Vì x₁ > 1; x₂ > 1 nên

Do đó hàm số y = 3/(x-1) nghịch biến trên khoảng (1; + ∞).

b) Với mọi x₁; x₂ ∈ (1; + ∞); x₁ ≠ x₂ ta có:

Vì x₁ > 1; x₂ > 1

nên hàm số y = x + 1/x đồng biến trên khoảng (1; + ∞).